
| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
分析 由$\overrightarrow{FA}=2\overrightarrow{AB}$,得$\overrightarrow{OA}$=$\frac{1}{3}$($\overrightarrow{OF}$+2$\overrightarrow{OB}$),从而求出A点坐标,再由点A在渐近线y=$\frac{b}{a}$x上,能求出双曲线的离心率.
解答 解:设点F(c,0),B(0,b),
由$\overrightarrow{FA}=2\overrightarrow{AB}$,得$\overrightarrow{OA}$=$\frac{1}{3}$($\overrightarrow{OF}$+2$\overrightarrow{OB}$),
∴A($\frac{c}{3}$,$\frac{2b}{3}$),
∵点A在渐近线y=$\frac{b}{a}$x上,则$\frac{2b}{3}$=$\frac{b}{a}$•$\frac{c}{3}$,
解得e=2.
故选:D.
点评 本题考查向量知识的运用,考查双曲线的离心率,利用向量知识确定A的坐标是关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
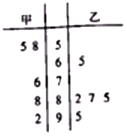 某校拟举办“成语大赛”,高一(1)班的甲、乙两名同学在本班参加:“成语大赛”选拔测试,在相同的测试条件下,两人5次测试的成绩(单位:分)的茎叶图如图所示:
某校拟举办“成语大赛”,高一(1)班的甲、乙两名同学在本班参加:“成语大赛”选拔测试,在相同的测试条件下,两人5次测试的成绩(单位:分)的茎叶图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (e,+∞) | C. | (-∞,-1) | D. | (-∞,-e) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{π}{6}]$ | B. | $(0,\frac{π}{3}]$ | C. | $[\frac{π}{6},π)$ | D. | $[\frac{π}{3},π)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.28J | B. | 0.12J | C. | 0.26J | D. | 0.18J |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数$f(x)=1+2sin(2x-\frac{π}{3})$.
已知函数$f(x)=1+2sin(2x-\frac{π}{3})$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com