
【题目】已知函数![]() , 则: (1)曲线
, 则: (1)曲线![]() 的斜率为
的斜率为![]() 的切线方程为__________;
的切线方程为__________;
(2)设![]() ,记
,记![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() .当
.当![]() 最小时,
最小时,![]() 的值为__________.
的值为__________.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点
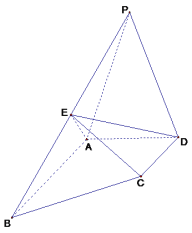
(1)求证:平面PAB⊥平面CDE;
(2)若AD=CD=2,求点P到平面ADE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是( )
A.若“![]() ”为假命题,则“
”为假命题,则“![]() ”为假命题
”为假命题
B.“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
C.命题“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
D.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于集合![]() ,定义函数
,定义函数![]() 对于两个集合
对于两个集合![]() ,定义集合
,定义集合![]() . 已知
. 已知![]() ,
, ![]() .
.
(Ⅰ)写出![]() 和
和![]() 的值,并用列举法写出集合
的值,并用列举法写出集合![]() ;
;
(Ⅱ)用![]() 表示有限集合
表示有限集合![]() 所含元素的个数,求
所含元素的个数,求![]() 的最小值;
的最小值;
(Ⅲ)有多少个集合对![]() ,满足
,满足![]() ,且
,且![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且2ccosB=2a+b.
(1)求角C的大小;
(2)若△ABC的面积等于![]() ,求ab的最小值.
,求ab的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式|x+1|>|2﹣x|+1的解集为M,且a,b,c∈M.
(1)比较|a﹣b|与|1﹣ab|的大小,并说明理由;
(2)若![]() ,求a2+b2+c2的最小值.
,求a2+b2+c2的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形几何学是一门以不规则几何形态为研究对象的几何学.分形的外表结构极为复杂,但其内部却是有规律可寻的.一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统.下面我们用分形的方法来得到一系列图形,如图1,线段![]() 的长度为
的长度为![]() ,在线段
,在线段![]() 上取两个点
上取两个点![]() ,
,![]() ,使得
,使得![]() ,以
,以![]() 为一边在线段
为一边在线段![]() 的上方做一个正六边形,然后去掉线段
的上方做一个正六边形,然后去掉线段![]() ,得到图2中的图形;对图2中的最上方的线段
,得到图2中的图形;对图2中的最上方的线段![]() 作相同的操作,得到图3中的图形;依此类推,我们就得到了以下一系列图形:
作相同的操作,得到图3中的图形;依此类推,我们就得到了以下一系列图形:
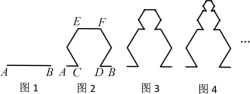
记第![]() 个图形(图1为第1个图形)中的所有线段长的和为
个图形(图1为第1个图形)中的所有线段长的和为![]() ,则(1)
,则(1)![]() ______;(2)如果对
______;(2)如果对![]() ,
,![]() 恒成立,那么线段
恒成立,那么线段![]() 的长度
的长度![]() 的取值范围是_______.
的取值范围是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com