已知函数f(x)=x-ax2-lnx(a>0).
(1)若曲线y=f(x)在点(1,f(1))处的切线斜率为-2,求a的值以及切线方程;
(2)若f(x)是单调函数,求a的取值范围.
解:(1)f′(x)=1-2ax-

.…(2分)
由题设,f′(1)=-2a=-2,a=1,
此时f(1)=0,切线方程为y=-2(x-1),即2x+y-2=0.…(5分)
(2)f′(x)=-
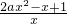
,
令△=1-8a.
当a≥

时,△≤0,f′(x)≤0,f(x)在(0,+∞)单调递减.…(10分)
当0<a<

时,△>0,方程2ax
2-x+1=0有两个不相等的正根x
1,x
2,
不妨设x
1<x
2,
则当x∈(0,x
1)∪(x
2,+∞)时,f′(x)<0,当x∈(x
1,x
2)时,f′(x)>0,
这时f(x)不是单调函数.
综上,a的取值范围是[

,+∞).…(12分)
分析:(1)先求函数f(x)的导数,再根据导数的几何意义列式求出a值,最后再根据直线的方程写出切线的方程即可.
(2)对函数求导,要讨论函数的单调性,只要讨论a的范围再判断f′(x)的符号即得.
点评:本题主要考查了利用函数的导数判断函数的单调性,导数的几何意义在切线的求解中的应用,属于中档试题

 .…(2分)
.…(2分)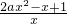 ,
, 时,△≤0,f′(x)≤0,f(x)在(0,+∞)单调递减.…(10分)
时,△≤0,f′(x)≤0,f(x)在(0,+∞)单调递减.…(10分) 时,△>0,方程2ax2-x+1=0有两个不相等的正根x1,x2,
时,△>0,方程2ax2-x+1=0有两个不相等的正根x1,x2, ,+∞).…(12分)
,+∞).…(12分)

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<