解:分情况讨论:
①△=a
2-16<0即-4<a<4时,2x
2+ax+2永远大于零,x取任意实数.
②△=a
2-16>0即a>4或a<-4时,对不等式2x
2+ax+2>0的左边进行因式分解得:
(x-
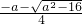
)(x-
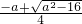
)>0
因为
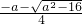
<
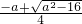
则 x>
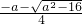
且x>
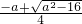
或x<
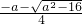
且x<
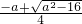
所以x>
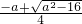
或x<
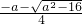
;
③△=a
2-16=0,即a=±4时,2x
2+ax+2=

>0,此时不等式的解集为x≠±1,
综上:当-4<a<4时,x取任意实数;
当a>4或a<-4时,为x>
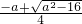
或x<
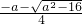
.
当a=4时,不等式解集为x≠-1;a=-4时,不等式解集为x≠1.
分析:先分析不等式左边的多项式求出△=a
2-16,分两种情况讨论其与零的大小关系来讨论不等式的解集,当△=a
2-16<0即-4<a<4时,2x
2+ax+2永远大于零,x取任意实数.当△=a
2-16≥0时又分两种情况讨论同号得正,同时为正或同时为负都可以,分别求出解集即可.
点评:考查学生分类讨论的思想,一元二次不等式的解法.

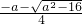 )(x-
)(x-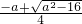 )>0
)>0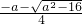 <
<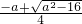
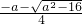 且x>
且x>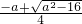 或x<
或x<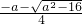 且x<
且x<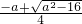
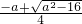 或x<
或x<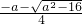 ;
; >0,此时不等式的解集为x≠±1,
>0,此时不等式的解集为x≠±1,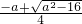 或x<
或x<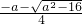 .
.
