
| A. | c<b<a | B. | b<a<c | C. | c<a<b | D. | a<b<c |
分析 设g(x)=$\frac{f(x)}{x}$,∵对任意两个不相等的正数x1,x2,都有$\frac{{x}_{2}f({x}_{1})-{x}_{1}f({x}_{2})}{{x}_{1}-{x}_{2}}$>0,可得g(x)在(0,+∞)上单调递增,分别化简a,b,c,即可得出结论.
解答 解:设g(x)=$\frac{f(x)}{x}$,∵对任意两个不相等的正数x1,x2,都有$\frac{{x}_{2}f({x}_{1})-{x}_{1}f({x}_{2})}{{x}_{1}-{x}_{2}}$>0,
∴g(x)在(0,+∞)上单调递增,
∵a=-log23•f(log${\;}_{\frac{1}{3}}$2)=g(log${\;}_{\frac{1}{3}}$2),b=f(1)=g(1),c=4f(0.52)=g(0.52),log${\;}_{\frac{1}{3}}$2<0<0.52<1,
∴c<a<b.
故选:C.
点评 本题考查大小比较,考查函数的单调性,考查学生分析解决问题的能力,正确构造函数是关键.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:解答题
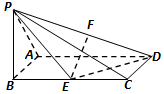 如图,已知PB⊥矩形ABCD所在的平面,E,F分别是BC,PD的中点,∠PAB=45°,AB=1,BC=2.
如图,已知PB⊥矩形ABCD所在的平面,E,F分别是BC,PD的中点,∠PAB=45°,AB=1,BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
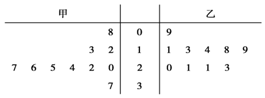 某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )
某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )| A. | 乙的众数是21 | B. | 甲的中位数是24 | ||
| C. | 甲的极差是29 | D. | 甲罚球命中率比乙高 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(千万元) | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
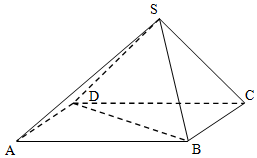 如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,且AB=2,SC=SD=$\sqrt{2}$.
如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,且AB=2,SC=SD=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{{2^n}+1}}{{{2^{n-1}}}}$ | B. | $\frac{{{2^n}-1}}{{{2^{n-1}}}}$ | C. | $\frac{{{2^n}+1}}{{{2^{n+1}}}}$ | D. | $\frac{{{2^n}-1}}{{{2^{n+1}}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com