
【题目】设数列{an}的前n项为Sn , 点(n, ![]() ),(n∈N*)均在函数y=3x﹣2的图象上.
),(n∈N*)均在函数y=3x﹣2的图象上.
(1)求数列{an}的通项公式.
(2)设bn= ![]() ,Tn为数列{bn}的前n项和,求使得Tn<
,Tn为数列{bn}的前n项和,求使得Tn< ![]() 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
【答案】
(1)解:依题意,点 ![]() 在y=3x﹣2的图象上,得
在y=3x﹣2的图象上,得 ![]() =3n﹣2,∴sn=3n2﹣2n;
=3n﹣2,∴sn=3n2﹣2n;
当n≥2时,an=Sn﹣Sn﹣1=(3n2﹣2n)﹣[3(n﹣1)2﹣2(n﹣1)]=6n﹣5 ①;
当n=1时,a1=S1=3×12﹣2=1,适合①式,所以,an=6n﹣5 (n∈N*)
(2)解:由(1)知,bn= ![]() =
= ![]() =
= ![]()
![]() ;
;
故Tn= ![]() =
= ![]()
![]() =
= ![]() ;
;
因此,使 ![]() 成立的m,必须且仅须满足
成立的m,必须且仅须满足 ![]() ,即m≥10;
,即m≥10;
所以,满足要求的最小正整数m为10
【解析】(1)由点 ![]() 在y=3x﹣2的图象上,得
在y=3x﹣2的图象上,得 ![]() =3n﹣2,即sn=3n2﹣2n;由an=Sn﹣Sn﹣1可得通项公式,须验证n=1时,an也成立.(2)由(1)知,bn=
=3n﹣2,即sn=3n2﹣2n;由an=Sn﹣Sn﹣1可得通项公式,须验证n=1时,an也成立.(2)由(1)知,bn= ![]() =…=
=…= ![]()
![]() ;求和Tn=
;求和Tn= ![]() ,可得
,可得 ![]() ;令
;令 ![]() ;即
;即 ![]() ,解得m即可.
,解得m即可.
【考点精析】根据题目的已知条件,利用等差数列的通项公式(及其变式)和数列的前n项和的相关知识可以得到问题的答案,需要掌握通项公式:![]() 或
或![]() ;数列{an}的前n项和sn与通项aspan>n的关系
;数列{an}的前n项和sn与通项aspan>n的关系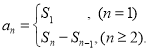 .
.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】设a<1,集合A={x∈R|x>0},B={x∈R|2x2﹣3(1+a)x+6a>0},D=A∩B.
(1)求集合D(用区间表示);
(2)求函数f(x)=x2﹣(1+a)x+a在D内的零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1个该产品获利润5元,未售出的产品,每个亏损3元.根据历史资料,得到开学季市场需求量的频率分布直方图如图所示.该同学为这个开学季购进了160个该产品,以![]() (
(![]() ,单位:个)表示这个开学季内的市场需求量.
,单位:个)表示这个开学季内的市场需求量.

(1)根据直方图估计这个开学季内市场需求量![]() 的中位数;
的中位数;
(2)根据直方图估计利润不少于640元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E,F,G,H分别为AA1 , AB,BB1 , B1C1的中点,则异面直线EF与GH所成的角等于 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4t,硝酸盐18t;生产1车乙种肥料的主要原料是磷酸盐1t、硝酸盐15t.现库存磷酸盐10t、硝酸盐66t.已知生产1车皮甲种肥料,产生的利润为10000元;生产1车皮乙种肥料,产生的利润为5000元.那么分别生产甲、乙两种肥料各多少车皮,能够产生最大利润?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a为实数,f(x)=(x2﹣4)(x﹣a).
(1)求导数f′(x);
(2)若f′(﹣1)=0,求f(x)在[﹣2,2]上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com