
【题目】已知函数![]() .
.
(1)求![]() 时,
时,![]() 的单调区间;
的单调区间;
(2)若存在![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]() ,求
,求![]() 的取值范围,并证明
的取值范围,并证明![]() .
.
【答案】(1)![]() 在
在![]() 为减函数,
为减函数,![]() 为增函数;(2)
为增函数;(2)![]() ,证明见解析
,证明见解析
【解析】
(1)由![]() 得
得![]() ,对函数求导,得到
,对函数求导,得到![]() , 令
, 令![]() ,用导数法方法判断其单调性,求出
,用导数法方法判断其单调性,求出![]() 在
在![]() 上为增函数,再由
上为增函数,再由![]() ,即可求出结果;
,即可求出结果;
(2)先对函数求导,得到 ,根据题意,得到
,根据题意,得到![]() 为
为![]() 在
在![]() 的极小值点,故
的极小值点,故![]() ,设
,设![]() ,对函数求导,根据函数单调性,得到
,对函数求导,根据函数单调性,得到 ,推出
,推出![]() ,再令
,再令![]() ,用导数的方法求出其单调性,进而可得出结果.
,用导数的方法求出其单调性,进而可得出结果.
(1)当![]() 时,
时,![]() ,
,
![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() ,由
,由![]() 得
得![]() ;由
;由![]() 得
得![]() ,
,
即函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
因此![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
即![]() 在
在![]() 上为增函数.
上为增函数.
又因为![]() ,
,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
故![]() 在
在![]() 为减函数,
为减函数,![]() 为增函数.
为增函数.
(2)  ,
,
因为![]() 对任意的
对任意的![]() 恒成立,所以
恒成立,所以![]() 为
为![]() 在
在![]() 的极小值点,故
的极小值点,故![]() ①.
①.
设![]() ,则当
,则当![]() 时,
时, ,
,
所以![]() 在
在![]() 上为增函数,而
上为增函数,而![]() ,
,![]() .
.
由①可知![]() ,从而
,从而![]() ,故
,故![]() .
.
又由 ,即
,即 ,
,
所以
![]() .
.
令![]() ,其中
,其中![]() ,则
,则![]() ,
,![]() 为
为![]() 上的减函数,
上的减函数,
故![]() ,而
,而![]() ,
,
所以![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,直角坐标系中,圆的方程为![]() ,
,![]() ,
,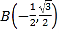 ,
,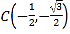 为圆上三个定点,某同学从
为圆上三个定点,某同学从![]() 点开始,用掷骰子的方法移动棋子.规定:①每掷一次骰子,把一枚棋子从一个定点沿圆弧移动到相邻下一个定点;②棋子移动的方向由掷骰子决定,若掷出骰子的点数为偶数,则按图中箭头方向移动;若掷出骰子的点数为奇数,则按图中箭头相反的方向移动.设掷骰子
点开始,用掷骰子的方法移动棋子.规定:①每掷一次骰子,把一枚棋子从一个定点沿圆弧移动到相邻下一个定点;②棋子移动的方向由掷骰子决定,若掷出骰子的点数为偶数,则按图中箭头方向移动;若掷出骰子的点数为奇数,则按图中箭头相反的方向移动.设掷骰子![]() 次时,棋子移动到
次时,棋子移动到![]() ,
,![]() ,
,![]() 处的概率分别为
处的概率分别为![]() ,
,![]() ,
,![]() .例如:掷骰子一次时,棋子移动到
.例如:掷骰子一次时,棋子移动到![]() ,
,![]() ,
,![]() 处的概率分别为
处的概率分别为![]() ,
,![]() ,
,![]() .
.
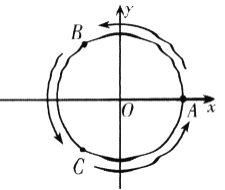
(1)分别掷骰子二次,三次时,求棋子分别移动到![]() ,
,![]() ,
,![]() 处的概率;
处的概率;
(2)掷骰子![]() 次时,若以
次时,若以![]() 轴非负半轴为始边,以射线
轴非负半轴为始边,以射线![]() ,
,![]() ,
,![]() 为终边的角的余弦值记为随机变量
为终边的角的余弦值记为随机变量![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)记![]() ,
,![]() ,
,![]() ,其中
,其中![]() .证明:数列
.证明:数列![]() 是等比数列,并求
是等比数列,并求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4,坐标系与参数方程】
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为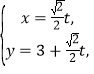 (t为参数),在以O为极点,
(t为参数),在以O为极点,![]() 轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为
轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为![]()
(Ⅰ)求直线![]() 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
(Ⅱ)若直线![]() 与
与![]() 轴的交点为P,直线
轴的交点为P,直线![]() 与曲线C的交点为A,B,求
与曲线C的交点为A,B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组
.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)求出![]() 的值;
的值;
(2)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种水果按照果径大小可分为四类:标准果、优质果、精品果、礼品果.某采购商从采购的一批水果中随机抽取![]() 个,利用水果的等级分类标准得到的数据如下:
个,利用水果的等级分类标准得到的数据如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
(1)若将频率视为概率,从这![]() 个水果中有放回地随机抽取
个水果中有放回地随机抽取![]() 个,求恰好有
个,求恰好有![]() 个水果是礼品果的概率;(结果用分数表示)
个水果是礼品果的概率;(结果用分数表示)
(2)用分层抽样的方法从这![]() 个水果中抽取
个水果中抽取![]() 个,再从抽取的
个,再从抽取的![]() 个水果中随机抽取
个水果中随机抽取![]() 个,
个,![]() 表示抽取的是精品果的数量,求
表示抽取的是精品果的数量,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】麻团又叫煎堆,呈球形,华北地区称麻团,是一种古老的中华传统特色油炸面食,寓意团圆。制作时以糯米粉团炸起,加上芝麻而制成,有些包麻茸、豆沙等馅料,有些没有。一个长方体形状的纸盒中恰好放入4个球形的麻团,它们彼此相切,同时与长方体纸盒上下底和侧面均相切,其俯视图如图所示,若长方体纸盒的表面积为576 ![]() ,则一个麻团的体积为_______
,则一个麻团的体积为_______![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com