
【题目】已知函数![]() ,
,![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)设函数![]() ,若存在
,若存在![]() ,对任意的
,对任意的![]() ,总有
,总有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;(2)实数
;(2)实数![]() 的取值范围为
的取值范围为![]() .
.
【解析】
试题分析:(1)首先确定函数的定义域,进一步对![]() 求导,利用导函数与原函数的关系,得到原函数的单调区间;(2)“存在
求导,利用导函数与原函数的关系,得到原函数的单调区间;(2)“存在![]() ,对任意的
,对任意的![]() ,总有
,总有![]() 成立”等价于“
成立”等价于“![]() 在
在![]() 上的最大值不小于
上的最大值不小于![]() 在
在![]() 上的最大值”进一步,分别求函数
上的最大值”进一步,分别求函数![]() 和
和![]() 在区间
在区间![]() 和
和![]() 上的最大值.
上的最大值.
试题解析:(1) ![]() ,(此处若不写定义域,可适当扣分)
,(此处若不写定义域,可适当扣分)
故![]() .
.
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
![]()
![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;
;
(2)![]() ,则
,则![]() ,
,
而![]() ,故在
,故在![]() 上
上![]() ,即函数
,即函数![]() 在
在![]() 上单调递增,
上单调递增,![]()
![]()
而“存在![]() ,对任意的
,对任意的![]() ,总有
,总有![]() 成立”等价于“
成立”等价于“![]() 在
在![]() 上的最大值不小于
上的最大值不小于![]() 在
在![]() 上的最大值”
上的最大值”
而![]() 在
在![]() 上的最大值为
上的最大值为![]() 中的最大者,记为
中的最大者,记为![]() .
.
所以有![]() ,
,![]() ,
,
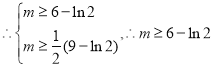 .
.
故实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知圆C:x2+(y﹣1)2=5,直线l:mx﹣y+1﹣m=0,且直线l与圆C交于A、B两点.
(1)若|AB|= ![]() ,求直线l的倾斜角;
,求直线l的倾斜角;
(2)若点P(1,1),满足2 ![]() =
= ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“幸”“福”“快”“乐”四个字,有放回地从中任取一个小球,取到“快”就停止,用随机模拟的方法估计直到第二次停止的概率:先由计算器产生1到4之间取整数值的随机数,且用1,2,3,4表示取出小球上分别写有“幸”“福”“快”“乐”四个字,以每两个随机数为一组,代表两次的结果,经随机模拟产生了20组随机数:
13 24 12 32 43 14 24 32 31 21
23 13 32 21 24 42 13 32 21 34
据此估计,直到第二次就停止的概率为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() (a>0,b>0)的右准线l2与一条渐近线l交于点P,F是双曲线的右焦点.
(a>0,b>0)的右准线l2与一条渐近线l交于点P,F是双曲线的右焦点.
(1)求证:PF⊥l;
(2)若PF=3,且双曲线的离心率e=![]() ,求该双曲线的方程.
,求该双曲线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设锐角△ABC的三内角A、B、C所对边的边长分别为a、b、c,且 a=1,B=2A,则b的取值范围为( )
A.( ![]() ,
, ![]() )
)
B.(1, ![]() )
)
C.( ![]() ,2)
,2)
D.(0,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种水杯,每个水杯的原材料费、加工费分别为30元、m元(m为常数,且2≤m≤3),设每个水杯的出厂价为x元(35≤x≤41),根据市场调查,水杯的日销售量与ex(e为自然对数的底数)成反比例,已知每个水杯的出厂价为40元时,日销售量为10个.
(1)求该工厂的日利润y(元)与每个水杯的出厂价x(元)的函数关系式;
(2)当每个水杯的出厂价为多少元时,该工厂的日利润最大,并求日利润的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=4,BC=2,D是BC的中点,若E是AB的中点,P是△ABC(包括边界)内任一点.则 ![]() 的取值范围是( )
的取值范围是( )
A.[﹣6,6]
B.[﹣9,9]
C.[0,8]
D.[﹣2,6]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两个分类变量x与y,其一组观测值如下面的2×2列联表所示:
y1 | y2 | |
x1 | a | 20-a |
x2 | 15-a | 30+a |
其中a,15-a均为大于5的整数,则a取何值时,在犯错误的概率不超过0.1的前提下认为x与y之间有关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com