

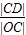 =
= ,∴|CD|=
,∴|CD|= t,∴f(t)=
t,∴f(t)= |OC|•|CD|=
|OC|•|CD|= t
t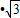 t=
t= .
. =
=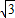 ,∴|MN|=
,∴|MN|= (2-t),
(2-t), •2•
•2• -
- •|AN|•|MN|=
•|AN|•|MN|= -
-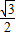 (2-t)2=-
(2-t)2=- +2
+2 t-
t-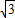 ;
;
 .
.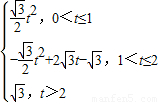 .
. .图象如图所示:
.图象如图所示: ;当1<t≤2时,
;当1<t≤2时, <f(t)≤
<f(t)≤ ;当t>2时,f(t)=
;当t>2时,f(t)= .所以f(t)的值域为(0,
.所以f(t)的值域为(0, ].
].

科目:高中数学 来源: 题型:
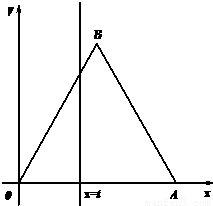
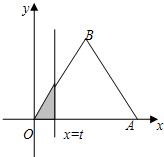 如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).试求函数f(t)的解析式,并画出函数y=f(t)的图象.
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).试求函数f(t)的解析式,并画出函数y=f(t)的图象.查看答案和解析>>
科目:高中数学 来源: 题型:
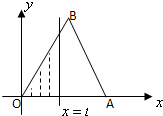 如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).查看答案和解析>>
科目:高中数学 来源: 题型:
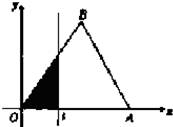 (2010•武汉模拟)如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积f(t),则函数f(t)的解析式为:
(2010•武汉模拟)如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积f(t),则函数f(t)的解析式为:
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com