
【题目】已知 ![]() 分别为
分别为 ![]() 内角的对边
内角的对边 ![]() ,
, ![]() .
.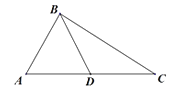
(1)若 ![]() 为
为 ![]() 的中点,求
的中点,求 ![]() ;
;
(2)若 ![]() ,判断
,判断 ![]() 的形状,并说明理由.
的形状,并说明理由.
科目:高中数学 来源: 题型:
【题目】已知圆C1:x2+y2=r2(r>0)与直线l0:y= ![]() 相切,点A为圆C1上一动点,AN⊥x轴于点N,且动点M满足
相切,点A为圆C1上一动点,AN⊥x轴于点N,且动点M满足 ![]() ,设动点M的轨迹为曲线C.
,设动点M的轨迹为曲线C.
(1)求动点M的轨迹曲线C的方程;
(2)若直线l与曲线C相交于不同的两点P、Q且满足以PQ为直径的圆过坐标原点O,求线段PQ长度的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程是 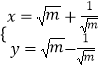 (m为参数),直线l交曲线C1于A,B两点;以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=4sin(θ﹣
(m为参数),直线l交曲线C1于A,B两点;以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=4sin(θ﹣ ![]() ),点P(ρ,
),点P(ρ, ![]() )在曲线C2上.
)在曲线C2上.
(1)求曲线C1的普通方程及点P的直角坐标;
(2)若直线l的倾斜角为 ![]() 且经过点P,求|PA|+|PB|的值.
且经过点P,求|PA|+|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,
, ![]() .
.
(1)求函数 ![]() 的单调增区间;
的单调增区间;
(2)若 ![]() ,解不等式
,解不等式 ![]() ;
;
(3)若 ![]() ,且对任意
,且对任意 ![]() ,方程
,方程 ![]() 在
在 ![]() 总存在两不相等的实数根,求
总存在两不相等的实数根,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中,真命题有 . (写出所有真命题的序号)
①若a,b,c∈R,则“ac2>bc2”是“a>b”成立的充分不必要条件;②命题“x0∈R, ![]() +x0+1<0”的否定是“x∈R,x2+x+1≥0”;③命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|<2,则-2<x<2”;④函数f(x)=ln x+x-
+x0+1<0”的否定是“x∈R,x2+x+1≥0”;③命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|<2,则-2<x<2”;④函数f(x)=ln x+x- ![]() 在区间(1,2)上有且仅有一个零点.
在区间(1,2)上有且仅有一个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩,老师说,你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩,看后甲对大家说:我还是不知道我的成绩,根据以上信息,则( )
A.乙可以知道两人的成绩
B.丁可能知道两人的成绩
C.乙、丁可以知道对方的成绩
D.乙、丁可以知道自己的成绩
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时,f(x)=x,则函数y=f(x)-log3|x|的零点个数是( )
A.多于4个
B.4个
C.3个
D.2个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=(x﹣2)(ax+b)为偶函数,且在(0,+∞)单调递增,则f(2﹣x)>0的解集为( )
A.{x|x>2或x<﹣2}
B.{x|﹣2<x<2}
C.{x|x<0或x>4}
D.{x|0<x<4}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com