
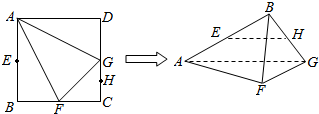
分析 (1)EH是△AFG的中位线,得EH∥AG,故EH∥平面AFG;
(2)因为折叠后B,C,D三点重合为一点B,故折叠后AB⊥BF,AB⊥BG可推出AB⊥平面BFG;
(3)连接EF,HF,则V棱锥F-AGHEV棱锥F=V棱锥F-AGB-V棱锥F-EHB.
解答 证明:(1)由题意可知点E、H在折叠前后都分别是AB、CG的中点(折叠后B、C两点重合),
∴EH∥AG,
∵EH?平面AFG,AG?平面AFG,
∴EH∥平面AFG.
(2)由题意可知AB⊥BF的关系在折叠前后都没有改变.
∵在折叠前AD⊥DG,由于折叠后AD与AB重合,点D与B重合,
∴AB⊥BG,
∵AB⊥BF,AB⊥BG,BF?平面BFG,BG?平面BFG,BF∩BG=B,
∴AB⊥平面BFG.
解:(3)∵折叠前BF⊥AB,CF⊥CG,∴折叠后BF⊥AB,BF⊥BG,
又∵AB∩BG=B,AB?平面ABG,BG?平面ABG,
∴BF⊥平面ABG.
∴V棱锥F-AGHE=V棱锥F-AGB-V棱锥F-EHB=$\frac{1}{3}$S△ABG•BF-$\frac{1}{3}$S△BEH•BF
=$\frac{1}{3}$×$\frac{1}{2}$×1×2×1-$\frac{1}{3}$×$\frac{1}{2}$×1×$\frac{1}{2}$×1=$\frac{1}{4}$.
点评 本题考查了线面平行,线面垂直的判定和空间几何体的体积计算,注意折叠前后的垂直关系不变是解决本题的关键.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,+∞) | B. | (3,$\frac{7}{2}$) | C. | (-∞,$\frac{7}{2}$] | D. | (0,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
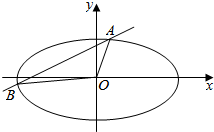 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,短轴的一个顶点与椭圆两焦点构成的三角形面积为2$\sqrt{3}$.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,短轴的一个顶点与椭圆两焦点构成的三角形面积为2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com