
 ,在B处投中为事件B,不中为事件
,在B处投中为事件B,不中为事件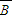 .则事件A,B相互独立,
.则事件A,B相互独立,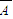 BB,由对立事件和相互独立事件性质,能求出甲同学测试结束后所得总分等于4的概率.
BB,由对立事件和相互独立事件性质,能求出甲同学测试结束后所得总分等于4的概率. )+P(
)+P(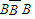 )+P(BB)的大小,再比较P2,P1的大小,从而得出结论.
)+P(BB)的大小,再比较P2,P1的大小,从而得出结论. ,
,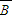 .则事件A,B相互独立,
.则事件A,B相互独立, BB,
BB,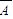 BB)=P(
BB)=P( )P(B)P(B)=0.5×0.8×0.8=0.32;
)P(B)P(B)=0.5×0.8×0.8=0.32;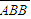 )=P(
)=P(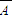 )P(
)P(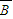 )P(
)P( )=0.5×0.2×0.2=0.02,
)=0.5×0.2×0.2=0.02, B
B )+P(
)+P( B)
B)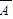 )P(B)P(
)P(B)P(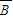 )+P(
)+P(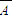 )P(
)P(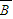 )P(B)
)P(B)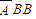 )=P(
)=P(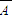 )P(B)P(B)=0.5×0.8×0.8=0.32,
)P(B)P(B)=0.5×0.8×0.8=0.32,
 )+P(
)+P(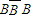 )+P(BB)=2×0.8×0.2+0.8×0.8=0.896,
)+P(BB)=2×0.8×0.2+0.8×0.8=0.896,

 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
| ξ | 0 | 2 | 3 | 4 | 5 |
| p | 0.03 | 0.24 | 0.01 | 0.48 | 0.24 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| ξ | 0 | 2 | 3 | 4 | 5 |
| p | 0.03 | P1 | P2 | P3 | P4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com