
已知函数f (x)=x3+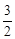 (1-a)x2-3ax+1,a>0.
(1-a)x2-3ax+1,a>0.
(Ⅰ) 证明:对于正数a,存在正数p,使得当x∈[0,p]时,有-1≤f (x)≤1;
(Ⅱ) 设(Ⅰ)中的p的最大值为g(a),求g(a)的最大值.
(Ⅰ)先利用导数求出单调区间,再分情况证明;
(Ⅱ) 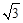
解析试题分析:
(Ⅰ) 由于f ′(x)=3x2+3(1-a)x-3a=3(x+1)(x-a),且a>0,
故f (x)在[0,a]上单调递减,在[a,+∞)上单调递增.
又f (0)=1,f (a)=- a3-
a3-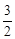 a2+1=
a2+1= (1-a)(a+2) 2-1.
(1-a)(a+2) 2-1.
当f (a)≥-1时,取p=a.
此时,当x∈[0,p]时有-1≤f (x)≤1成立.
当f (a)<-1时,由于f (0)+1=2>0,f (a)+1<0,
故存在p∈(0,a)使得f (p)+1=0.
此时,当x∈[0,p]时有-1≤f (x)≤1成立.
综上,对于正数a,存在正数p,使得当x∈[0,p]时,有-1≤f (x)≤1. 7分
(Ⅱ) 由(Ⅰ)知f (x)在[0,+∞)上的最小值为f (a).
当0<a≤1时,f (a)≥-1,则g(a)是方程f (p)=1满足p>a的实根,
即2p2+3(1-a)p-6a=0满足p>a的实根,所以
g(a)=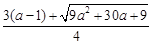 .
.
又g(a)在(0,1]上单调递增,故g(a)max=g(1)=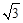 .
.
当a>1时,f (a)<-1.
由于f (0)=1,f (1)=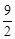 (1-a)-1<-1,故[0,p]Ì [0,1].
(1-a)-1<-1,故[0,p]Ì [0,1].
此时,g(a)≤1.
综上所述,g(a)的最大值为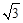 . 15分
. 15分
考点:本题主要考查利用导数研究函数的性质等基础知识,同时考查推理论证能力,分类讨论等综合解题能力和创新意识。
点评:研究函数的性质往往离不开导数,导数是研究函数性质的有力工具,要灵活运用;另外,函数如果含参数,一般离不开分类讨论,分类讨论时要做到不重不漏.


科目:高中数学 来源: 题型:解答题
已知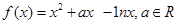 .
.
(1)若a=0时,求函数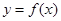 在点(1,
在点(1, )处的切线方程;
)处的切线方程;
(2)若函数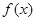 在[1,2]上是减函数,求实数a的取值范围;
在[1,2]上是减函数,求实数a的取值范围;
(3)令 是否存在实数a,当
是否存在实数a,当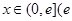 是自然对数的底)时,函数
是自然对数的底)时,函数 的最小值是3,若存在,求出a的值;若不存在,说明理由.
的最小值是3,若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=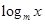 (m为常数0<m<1),且数列{f(
(m为常数0<m<1),且数列{f(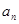 )}是首项为2,公差为2的等差数列.
)}是首项为2,公差为2的等差数列.
(1)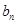 =
=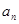 f(
f(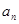 ),当m=
),当m=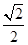 时,求数列{
时,求数列{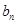 }的前n项和
}的前n项和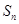 ;
;
(2)设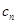 =
=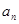 ·
·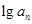 ,如果{
,如果{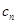 }中的每一项恒小于它后面的项,求m的取值范围.
}中的每一项恒小于它后面的项,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,
, (其中
(其中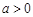 ).
).
(Ⅰ)求函数 的极值;
的极值;
(Ⅱ)若函数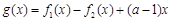 在区间
在区间 内有两个零点,求正实数a的取值范围;(Ⅲ)求证:当
内有两个零点,求正实数a的取值范围;(Ⅲ)求证:当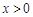 时,
时, .(说明:e是自然对数的底数,e=2.71828…)
.(说明:e是自然对数的底数,e=2.71828…)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com