
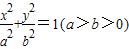 上一点M向x轴作垂线,恰好通过椭
上一点M向x轴作垂线,恰好通过椭
 .再根据点M在椭圆上,
.再根据点M在椭圆上, ,再结合AO=a,BO=b,OF1=c,代入所得比例式,化简可得b=c,从而求出椭圆的离心率e;
,再结合AO=a,BO=b,OF1=c,代入所得比例式,化简可得b=c,从而求出椭圆的离心率e; .最后综合,得到
.最后综合,得到 ,即为∠F1QF2的取值范围.
,即为∠F1QF2的取值范围. …(*)
…(*) ,
, ,解之得y1=
,解之得y1= (舍负),所以MF1=
(舍负),所以MF1= ,
, ,
, ,可得
,可得 (舍负)(8分)
(舍负)(8分) 
 ,
, =a2,即得2QF1•QF2(1+cosθ)≤2a2(1+cosθ),
=a2,即得2QF1•QF2(1+cosθ)≤2a2(1+cosθ), ,
, ,即∠F1QF2的取值范围是
,即∠F1QF2的取值范围是 (14分)
(14分)

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:
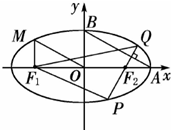 (普通班)如图所示,从椭圆
(普通班)如图所示,从椭圆| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源:2013届甘肃省高二12月月考文科数学试卷 题型:解答题
(普通班)如图所示,从椭圆 上一点M向
上一点M向 轴作垂线,恰好通过椭圆的左焦点
轴作垂线,恰好通过椭圆的左焦点 ,且它的长轴端点A及短轴端点B的连线
,且它的长轴端点A及短轴端点B的连线 .
.

(1) 求椭圆的离心率e;
(2) 设Q是椭圆上任意一点, 是右焦点,
是右焦点, 是左焦点,求
是左焦点,求 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
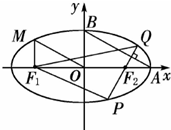 (普通班)如图所示,从椭圆
(普通班)如图所示,从椭圆 上一点M向x轴作垂线,恰好通过椭
上一点M向x轴作垂线,恰好通过椭查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com