Question

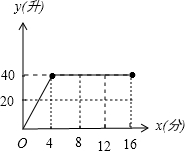
（2006•静安区二模）某种洗衣机在洗涤衣服时，需经过进水、清洗、排水、脱水四个连续的过程．假设进水时水量匀速增加，清洗时水量保持不变．已知进水时间为4分钟，清洗时间为12分钟，排水时间为2分钟，脱水时间为2分钟．洗衣机中的水量y（升）与时间x（分钟）之间的关系如下表所示：

x	0	2	4	16	16.5	17	18	…
y	0	20	40	40	29.5	20	2	…

请根据表中提供的信息解答下列问题：
（1）试写出当x∈[0，16]时y关于x的函数解析式，并画出该函数的图象；
（2）根据排水阶段的2分钟点（x，y）的分布情况，可选用y=

a

x

+b或y=c（x-20）²+d（其中a、b、c、d为常数），作为在排水阶段的2分钟内水量y与时间x之间关系的模拟函数．试分别求出这两个函数的解析式；
（3）请问（2）中求出的两个函数哪一个更接近实际情况？（写出必要的步骤）

Answer 1

分析：（1）由图表看出当x∈[0，4]时y关于x的函数为一次函数，当x∈（4，16]时y关于x的函数为常数函数，由图表直接写出函数解析式；
（2）用表中数据代入y=

a

x

+b和y=c（x-20）²+d求出具体解析式；
（3）从表中取以数据分别代入两个函数解析式求值验证．

解答：解：（1）当x∈[0，16]时，函数解析式为：
y=

10x，0≤x≤4 40，4＜x≤16

；
图象如图，

（2）①设y=

a

x

+b，由表中数据可得：

29.5= a 16.5 +b 20= a 17 +b

，解得

a=5329.5 b=-293.5

．
∴函数解析式为：y=

5329.5

x

-293.5．
②设y=c（x-20）²+d，
由表中数据可得

29.5=c(16.5-20)2+d 20=c(17-20)2+d

，解得

c=2-923 d=-6.307

．
∴函数解析式为：y=2.923（x-20）²-6.307．
（3）将x=18分别代入y1=

5329.5

x

-293.5，y2=2.923(x-20)2-6.307，
得y₁=2.6，y₂=5.385
原表实际情况为x=18时，y=2，|2-2.6|=0.6＜|2-5.385|3.385．
显然y=

5329.5

x

-293.5更接近实际情况．

点评：本题考查了函数模型的选择与应用，综合考查了函数与方程的思想方法，是中档题．