
【题目】如图,在三棱台ABC﹣A1B1C1中,CC1⊥平面ABC,AB=2A1B1=2CC1 , M,N分别为AC,BC的中点. 
(1)求证:AB1∥平面C1MN;
(2)若AB⊥BC且AB=BC,求二面角C﹣MC1﹣N的大小.
【答案】
(1)证明:连接B1N,B1C,
设B1C与NC1交于点G,在三棱台ABC﹣A1B1C1中,
AB=2A1B1,则BC=2B1C1,
而N是BC的中点,B1C1∥BC,
则B1C1 ![]() NC,所以四边形B1C1CN是平行四边形,G是B1C的中点,
NC,所以四边形B1C1CN是平行四边形,G是B1C的中点,
在△AB1C中,M是AC的中点,则MG∥AB1,
又AB1平面C1MN,MG平面C1MN,
所以AB1∥平面C1MN
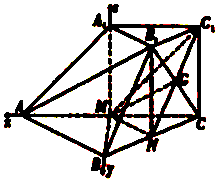
(2)解:由CC1⊥平面ABC,可得A1M⊥平面ABC,
而AB⊥BC,AB=BC,则MB⊥AC,
所以MA,MB,MA1两两垂直,
故以点M为坐标原点,MA,MB,MA1所在的直线分别为x,y,z轴建立如图所示的空间直角坐标系.
设AB=2,则A1B1=CC1=1,AC=2 ![]() ,AM=
,AM= ![]() ,
,
B(0, ![]() ,0),C(﹣
,0),C(﹣ ![]() ,0,0),C1(﹣
,0,0),C1(﹣ ![]() ,0,1),N(﹣
,0,1),N(﹣ ![]() ,
, ![]() ,0),
,0),
则平面ACC1A1的一个法向量为 ![]() =(0,1,0),
=(0,1,0),
设平面C1MN的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 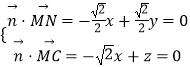 ,
,
取x=1,则 ![]() =(1,1,
=(1,1, ![]() ),
),
cos< ![]() >=
>= ![]() ,
,
由图形得得二面角C﹣MC1﹣N为锐角,
所以二面角C﹣MC1﹣N的大小为60°.
【解析】(1)连接B1N,B1C,设B1C与NC1交于点G,推导出四边形B1C1CN是平行四边形,从而MG∥AB1 , 由此能证明AB1∥平面C1MN.(2)以点M为坐标原点,MA,MB,MA1所在的直线分别为x,y,z轴建立空间直角坐标系,利用向量法能求出二面角C﹣MC1﹣N的大小.
【考点精析】通过灵活运用直线与平面平行的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行即可以解答此题.


科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和记为Sn且满足Sn=2an﹣1,n∈N*;
(1)求数列{an}的通项公式;
(2)设Tn=a1a2﹣a2a3+a3a4﹣a4a5+…+(﹣1)n+1anan+1 , 求{Tn}的通项公式;
(3)设有m项的数列{bn}是连续的正整数数列,并且满足:lg2+lg(1+ ![]() )+lg(1+
)+lg(1+ ![]() )+…+lg(1+
)+…+lg(1+ ![]() )=lg(log2am).
)=lg(log2am).
问数列{bn}最多有几项?并求出这些项的和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)的表达式为f(x)= ![]() (c≠0),则函数f(x)的图象的对称中心为(﹣
(c≠0),则函数f(x)的图象的对称中心为(﹣ ![]() ,
, ![]() ),现已知函数f(x)=
),现已知函数f(x)= ![]() ,数列{an}的通项公式为an=f(
,数列{an}的通项公式为an=f( ![]() )(n∈N),则此数列前2017项的和为 .
)(n∈N),则此数列前2017项的和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若偶函数f(x)在(﹣∞,0]上单调递减,a=f(log23),b=f(log45),c=f(2 ![]() ),则a,b,c满足( )
),则a,b,c满足( )
A.a<b<c
B.b<a<c
C.c<a<b
D.c<b<a
查看答案和解析>>
科目:高中数学 来源: 题型:
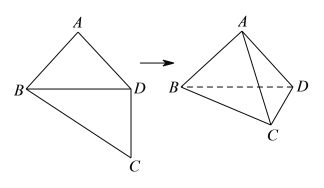
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,将四边形
,将四边形![]() 沿对角线
沿对角线![]() 折成四面
折成四面![]() .使平面
.使平面![]() 平面
平面![]() ,则下列结论正确的是( ).
,则下列结论正确的是( ).
A. ![]() B.
B. ![]()
C. ![]() 与平面
与平面![]() 所成的角为
所成的角为![]() D. 四面体
D. 四面体![]() 的体积为
的体积为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系xOy中,以O为极点,x轴的非负半轴为极轴建立极坐标系,P点的极坐标为(3, ![]() ).曲线C的参数方程为ρ=2cos(θ﹣
).曲线C的参数方程为ρ=2cos(θ﹣ ![]() )(θ为参数).
)(θ为参数).
(Ⅰ)写出点P的直角坐标及曲线C的直角坐标方程;
(Ⅱ)若Q为曲线C上的动点,求PQ的中点M到直线l:2ρcosθ+4ρsinθ= ![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,an+1= ![]() (n∈N*).
(n∈N*).
(1)求证:{ ![]() +
+ ![]() }为等比数列,并求{an}的通项公式an;
}为等比数列,并求{an}的通项公式an;
(2)数列{bn}满足bn=(3n﹣1) ![]() an , 求数列{bn}的前n项和Tn .
an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人们生活水平的不断提高,人们对餐饮服务行业的要求也越来越高,由于工作繁忙无法抽出时间来享受美味,这样网上外卖订餐应运而生.若某商家的一款外卖便当每月的销售量![]() (单位:千盒)与销售价格
(单位:千盒)与销售价格![]() (单位:元/盒)满足关系式
(单位:元/盒)满足关系式![]() 其中
其中![]() ,
,![]() 为常数,已知销售价格为14元/盒时,每月可售出21千盒.
为常数,已知销售价格为14元/盒时,每月可售出21千盒.
(1)求![]() 的值;
的值;
(2)假设该款便当的食物材料、员工工资、外卖配送费等所有成本折合为每盒12元(只考虑销售出的便当盒数),试确定销售价格![]() 的值,使该店每月销售便当所获得的利润最大.(结果保留一位小数)
的值,使该店每月销售便当所获得的利润最大.(结果保留一位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)已知函数f(x)=ax2+bx+c(a>0,b∈R,c∈R).
(1)若函数f(x)的最小值是f(-1)=0,且c=1, F(x)=![]() 求F(2)+F(-2)的值;
求F(2)+F(-2)的值;
(2)若a=1,c=0,且|f(x)|≤1在区间(0,1]上恒成立,试求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com