
����Ŀ��ij��ʳƷҩƷ�ල�����ֿ�չ2019�괺��У������ȫ��飬�Ա��е�8����ѧʳ�ý�����ԭ�ϲɹ��ӹ������������ļ������֣�������������±���ʾ��
��ѧ��� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
ԭ�ϲɹ��ӹ�������x | 100 | 95 | 93 | 83 | 82 | 75 | 70 | 66 |
����������y | 87 | 84 | 83 | 82 | 81 | 79 | 77 | 75 |
��1����֪x��y֮�����������ع�ϵ����y����x�����Իع鷽�̣�����ȷ��0.1��
��2���ִ�8����������ѧʳ���������ȡ�������һ�飬��������ѧʳ�õ�ԭ�ϲɹ��ӹ����������������־�����80�֣�����ɡ��Աȱ��ʳ�á�������鱻��Ϊ���Աȱ��ʳ�á��ĸ���.
�ο���ʽ�� ��
��![]() ��
��
�ο����ݣ�![]() ��
��![]() .
.
���𰸡���1��![]() ����2��
����2��![]()
��������
��1�����������![]() ��
��![]() ������ع�ϵ����д�����Իع鷽�̣�
������ع�ϵ����д�����Իع鷽�̣�
��2�����оٷ�д�������¼�������������ĸ���ֵ��
��1��������ã�![]() ��
��![]() ��
��
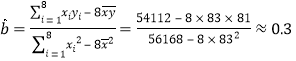 ��
��
![]() .
.
����������Իع鷽��Ϊ��![]() .
.
��2����8����ѧʳ������ѡ���������й�28�ֽ����
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
����ԭ�ϲɹ��ӹ��������ֺ������������־�����80�ֵ���10�ֽ����
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
���Ը��鱻��Ϊ���Աȱ��ʳ�á��ĸ���Ϊ![]() .
.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��2��22�գ��ں���ƽ�����»�̵��ٻ�����500�ױ����У��й�ѡ��������������������¼��������֣�Ϊ�й������Ӷ���˱��춬�»����ö���ƣ�Ҳ�����й����ӱ��Ͼ�����Ŀ�ڶ��»�������ͻ��.ij��УΪ�����Уѧ���ڶ��»��ڼ��ۼƹۿ����»��ʱ��������ռ���200λ������100λŮ���ۼƹۿ����»�ʱ����������ݣ���λ��Сʱ��.����100λŮ���������ȡ20���ˣ���֪��20λŮ�������ݾ�Ҷͼ��ͼ��ʾ.
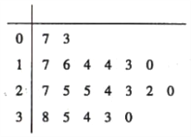

��I������20λŮ����ʱ�����ݷֳ�8�飬��������ֱ�Ϊ![]()
![]() ��
��![]() ������
������![]() ��
��![]()
![]() �����Ƶ�ʷֲ�ֱ��ͼ��
�����Ƶ�ʷֲ�ֱ��ͼ��
��II���ԣ�I���е�Ƶ����Ϊ���ʣ���1��Ů���ۿ����»�ʱ�䲻����30Сʱ�ĸ��ʣ���III���ԣ�I���е�Ƶ�ʹ���100λŮ�����ۼƹۿ�ʱ��С��20��Сʱ����������֪200λ�������ۼƹۿ�ʱ��С��20Сʱ��������50��.���������������������ж��Ƿ���99%�İ�����Ϊ����Уѧ���ۿ����»��ۼ�ʱ�����Ա��йء�.
���� | �� |
| |
�ۼƹۿ�ʱ��С��20Сʱ | |||
�ۼƹۿ�ʱ��С��20Сʱ | |||
�ܼ� | 300 |
������![]()
![]() ��.
��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x2��2x+alnx��a��0����
����a=2ʱ��������ͼ�߹��㣨1��f��1���������߷��̣�
����a=1ʱ��������x�ķ���f��x��=x+b��Ψһʵ���⣬����ʵ��b��ȡֵ��Χ��
����������f��x����������ֵ��x1��x2��x1��x2�����Ҳ���ʽf��x1����mx2�����������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ����������ԭ��Ϊ������x ���������Ϊ���Ὠ��������ϵ����֪����C1 �ķ���Ϊ��=2cos��+2sin�ȣ�ֱ�� C2 �IJ�������Ϊ![]() ��t Ϊ������
��t ������
���� C1 �ķ��̻�Ϊֱ�����귽�̣�
������P Ϊ C1 ��һ���㣬�� P ��ֱ�� C2 �ľ�������ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊѡ��һ��ѧ���μ�ȫ��ʵ������ܾ�����A��B��λͬѧ��ѧУ��ѧϰ�����ֳ����мӹ�ֱ��Ϊ20mm��������ԣ��������ӹ���10�����ֱ�������������ͼ��ʾ����λ��mm��

A��B��λͬѧ���ӹ���10�����ֱ����ƽ�����뷽�������±���
ƽ���� | ���� | |
A | 20 | 0.016 |
B | 20 | s2B |
���ݲ��Եõ����й����ݣ��Խ���������⣺
������s2B������ƽ�����뷽�˵��˭�ijɼ���Щ��
������ͼ�������������������Ϊ��˭ȥ�����Ϻ��ʣ���˵��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���ԭ��OΪ���㣬x��ķǸ�����Ϊ���ᣬ����������ϵ����ֱ��l�IJ�������Ϊ ![]() ��tΪ��������Ϊl����б�ǣ�������E�ļ����귽��Ϊ��=4sin�ȣ����ߦ�=�£���=��+
��tΪ��������Ϊl����б�ǣ�������E�ļ����귽��Ϊ��=4sin�ȣ����ߦ�=�£���=��+ ![]() ����=�©�
����=�©� ![]() ������E�ֱ��ڲ�ͬ�ڼ��������A��B��C��
������E�ֱ��ڲ�ͬ�ڼ��������A��B��C��
��1����֤��|OB|+|OC|= ![]() |OA|��
|OA|��
��2������= ![]() ʱ��ֱ��l��B��C���㣬��y0�����ֵ��
ʱ��ֱ��l��B��C���㣬��y0�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪Բ
�У���֪Բ![]() ��
��![]() ��Բ
��Բ![]() ��
��![]() ������
������![]() ��ֱ��
��ֱ��![]() ��
��![]() �ϣ�
�ϣ�![]() ������
������![]() �ֱ���Բ
�ֱ���Բ![]() ��
��![]() �����ߣ��е�ֱ�Ϊ
�����ߣ��е�ֱ�Ϊ![]() ��
��![]() ��������
��������![]() �ĵ�
�ĵ�![]() ����ֻ��һ������ʵ��
����ֻ��һ������ʵ��![]() ��ֵΪ______.
��ֵΪ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����������ABCD�ĵ�A����60�㣮ֱ������ADEF���ڵ�ƽ�洹ֱ��ƽ�� ABCD����EDA=90�㣬��ED=AD=2AF=2AB=2��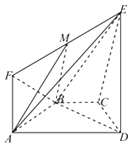
����֤����ƽ��ABE��ƽ��EBD��
����M���߶�EF�ϣ���ȷ����M��λ�ã�ʹƽ��MAB��ƽ��ECD���ɵĽǵ�����ֵΪ ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
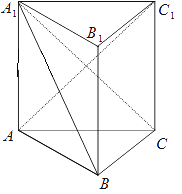
����Ŀ����ͼ��������ABC��A1B1C1�У�AA1��ƽ��ABC��AA1=AC=2BC����ACB=90�㣮
������֤��AC1��A1B��
������ֱ��AB��ƽ��A1BC���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com