练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设集合＝{1，2，3，…，n}(其中n≥3，n)，将的所有3元子集（含有3个元素的子集）中的最小元素的和记为.

    （1）求，，的值；

    （2）试求的表达式.

    【答案】（1）；；（2）

    【解析】

    （1）根据的所有3元子集（含有3个元素的子集）中的最小元素的和记为，得到， ，，再求，，的值.

    （2）根据三元子集的定义，最小元素为1的三元子集个数为，最小元素为2的三元子集个数为，最小元素为3的三元子集个数为，……最小元素为n﹣2的三元子集个数为，则，然后利用性质求解.

    （1），其所有三元子集为，故；

    ，其所有三元子集为，，，，故；

    ，，其所有三元子集为，，，，，，，，，，故；

    （2）的所有三元子集中：

    最小元素为1的三元子集个数为

    最小元素为2的三元子集个数为

    最小元素为3的三元子集个数为

    ……

    最小元素为n﹣2的三元子集个数为

    ……

    .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数，其中．

    （Ⅰ）试讨论的单调性；

    （Ⅱ）若函数存在极值，对于任意的，存在正实数，使得 ，试判断与的大小关系并给出证明.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是边长为2的正三角形，是等腰直角三角形.把沿其斜边翻折到，使，设为的中点.

    （1）求证：平面平面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某运动制衣品牌为了成衣尺寸更精准，现选择15名志愿者，对其身高和臂展进行测量（单位：厘米），左图为选取的15名志愿者身高与臂展的折线图，右图为身高与臂展所对应的散点图，并求得其回归方程为，以下结论中不正确的为

    A. 15名志愿者身高的极差小于臂展的极差

    B. 15名志愿者身高和臂展成正相关关系，

    C. 可估计身高为190厘米的人臂展大约为189.65厘米，

    D. 身高相差10厘米的两人臂展都相差11.6厘米，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1是淋浴房示意图，它的底座是由正方形截去一角得到，这一角是一个与正方形两邻边相切的圆的圆弧（如图2）.现已知正方形的边长是1米，设该底座的面积为S平方米，周长为l米（周长是指图2中实线部分），圆的半径为r米.设计的理想要求是面积S尽可能大，周长l尽可能小，但显然S、l都是关于r的减函数，于是设，当的值越大，满意度就越高.试问r为何值时，该淋浴房底座的满意度最高？（解答时π以3代入运算）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】空气质量指数AQI是反映空气质量状况的指数，AQI指数值越小，表明空气质量越好，其对应关系如下表：

    AQI指数值

    0～50

    51～100

    101～150

    151～200

    201～300

    ＞300

    空气质量

    优

    良

    轻度污染

    中度污染

    重度污染

    严重污染

    下图是某市10月1日—20日AQI指数变化趋势：

    下列叙述错误的是

    A. 这20天中AQI指数值的中位数略高于100

    B. 这20天中的中度污染及以上的天数占

    C. 该市10月的前半个月的空气质量越来越好

    D. 总体来说，该市10月上旬的空气质量比中旬的空气质量好

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业通过调查问卷（满分50分）的形式对本企业900名员工的工作满意程度进行调查，并随机抽取了其中30名员工（16名女工，14名男工）的得分，如下表：

    女

    47

    36

    32

    48

    34

    44

    43

    47

    46

    41

    43

    42

    50

    43

    35

    49

    男

    37

    35

    34

    43

    46

    36

    38

    40

    39

    32

    48

    33

    40

    34

    （1）根据以上数据，估计该企业得分大于45分的员工人数；

    （2）现用计算器求得这30名员工的平均得分为40.5分，若规定大于平局得分为 “满意”，否则为 “不满意”，请完成下列表格：

    “满意”的人数

    “不满意”的人数

    合计

    女员工

    16

    男员工

    14

    合计

    30

    （3）根据上述表中数据，利用独立性检验的方法判断，能否在犯错误的概率不超过1%的前提下，认为该企业员工“性别”与“工作是否满意”有关？

    参考数据：

    P(K2K)

    0.10

    0.050

    0.025

    0.010

    0.001

    K

    2.706

    3.841

    5.024

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中为自然对数的底数.

    （1）讨论函数在区间上的单调性；

    （2）已知，若对任意，有，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】火箭少女101的新曲《卡路里》受到了广大听众的追捧，歌词积极向上的体现了人们对于健康以及完美身材的渴望．据有关数据显示，成年男子的体脂率在14%-25%之间．几年前小王重度肥胖，在专业健身训练后，身材不仅恢复正常，且走上美体路线．通过整理得到如下数据及散点图．

    健身年数

    1

    2

    3

    4

    5

    6

    体脂率（有分比）

    32

    20

    12

    8

    6.4

    4.4

    3.4

    3

    2.5

    2.1

    1.9

    1.5

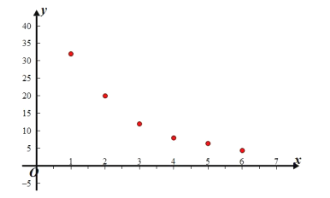
    （1）根据散点图判断，与哪一个模型更适宜作为体脂率关于健身年数的回归方程模型（给出选择即可）

    （2）根据（1）的判断结果与题目中所给数据，建立与的回归方程.（保留一位小数）

    （3）再坚持3年，体脂率可达到多少．

    参考公式：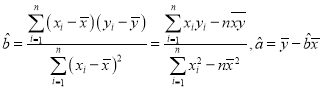

    参考数据：

    查看答案和解析>>

    同步练习册答案