
分析 设A(x1,y1),B(x2,y2).直线方程与椭圆方程联立化为(2+k2)x2+4kx+2=0.△>0,解得k2>2.利用斜率计算公式、根与系数的关系代入kOA+kOB=3,即可解出.
解答 解:设A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{y=kx+2}\\{{x}^{2}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,化为(2+k2)x2+4kx+2=0.
△=16k2-8(2+k2)=8k2-16>0,解得k2>2.
∴x1+x2=$\frac{-4k}{2+{k}^{2}}$,x1x2=$\frac{2}{2+{k}^{2}}$.
∵kOA+kOB=3,
∴$\frac{{y}_{1}}{{x}_{1}}+\frac{{y}_{2}}{{x}_{2}}$=$\frac{k{x}_{1}+2}{{x}_{1}}$+$\frac{k{x}_{2}+2}{{x}_{2}}$=2k+$\frac{2({x}_{1}+{x}_{2})}{{x}_{1}{x}_{2}}$=2k+2×$\frac{\frac{-4k}{2+{k}^{2}}}{\frac{2}{1+{k}^{2}}}$=3,
化为:-2k=3,
解得k=-$\frac{3}{2}$,满足△>0.
故答案为:-$\frac{3}{2}$.
点评 本题考查了直线与椭圆相交问题、斜率计算公式、一元二次方程的根与系数的关系,考查了变形能力与计算能力,属于中档题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 工作代码 | 紧前工作 | 工期(天) |
| A | 无 | 7 |
| B | 无 | 3 |
| C | 无 | 1 |
| D | C | 3 |
| E | A,B,D | 3 |
| F | E | 2 |
| G | A,B,D | 2 |
| H | F,G | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
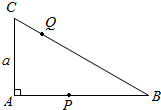 如图,在Rt△ABC中,∠B=30°,∠C=60°,AC=a,动点P,Q自A出发分别沿边界按ABCA的方向及ACBA的方向运动,它们的速度之比是1:3,当P,Q相遇时,停止运动,点P所走过的路程为x,△APQ的面积为y,写出y关于x的函数关系式,并求出定义域.
如图,在Rt△ABC中,∠B=30°,∠C=60°,AC=a,动点P,Q自A出发分别沿边界按ABCA的方向及ACBA的方向运动,它们的速度之比是1:3,当P,Q相遇时,停止运动,点P所走过的路程为x,△APQ的面积为y,写出y关于x的函数关系式,并求出定义域.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com