Question

14．在四面体S-ABC中，SA=8，SB=10，SC=AB=BC=CA=6，A′，B′，C′分别是棱SA，SB，SC上的点，且SA′=2，SB′=2.5，SC′=4，则截面A′B′C′将四面体S-ABC分成的两部分体积之比为（　　）

• A． $\frac{1}{24}$
• B． $\frac{1}{23}$
• C． $\frac{1}{9}$
• D． $\frac{1}{8}$

Answer 1

分析 由已知得$\frac{{V}_{S-{A}^{'}{B}^{'}{C}^{'}}}{{V}_{S-ABC}}$=$\frac{{V}_{{B}^{'}-S{A}^{'}{C}^{'}}}{{V}_{B-SAC}}$，由此利用棱锥体积计算公式和正弦定理能求出截面A′B′C′将四面体S-ABC分成的两部分体积之比．

解答 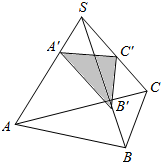解：∵在四面体S-ABC中，SA=8，SB=10，SC=AB=BC=CA=6，
A′，B′，C′分别是棱SA，SB，SC上的点，且SA′=2，SB′=2.5，SC′=4，
∴$\frac{{V}_{S-{A}^{'}{B}^{'}{C}^{'}}}{{V}_{S-ABC}}$=$\frac{{V}_{{B}^{'}-S{A}^{'}{C}^{'}}}{{V}_{B-SAC}}$=$\frac{\frac{1}{3}×{S}_{△S{A}^{'}{C}^{'}}×{h}_{{B}^{'}}}{\frac{1}{3}×{S}_{SAC}×{h}_{B}}$
=$\frac{\frac{1}{2}×S{A}^{'}×S{C}^{'}×sin∠{A}^{'}S{C}^{'}}{\frac{1}{2}×SA×SC×sin∠ASC}•\frac{S{B}^{'}}{SB}$
=$\frac{S{A}^{'}×S{C}^{'}×S{B}^{'}}{SA×SC×SB}$
=$\frac{2×4×2.5}{8×6×10}$
=$\frac{1}{24}$，
∴$\frac{{V}_{S-{A}^{'}{B}^{1}{C}^{'}}}{{V}_{ABC-{A}^{'}{B}^{'}{C}^{'}}}$=$\frac{1}{23}$．
故选：B．

点评 本题考查平面截棱锥所得两部分体积之比的求法，是中档题，解题时要认真审题，注意等体积法的合理运用．