
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() 为
为![]() 中点,底面
中点,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)设![]() 为棱
为棱![]() 上一点,
上一点,![]() ,试确定
,试确定![]() 的值使得二面角
的值使得二面角![]() 为
为![]() .
.
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
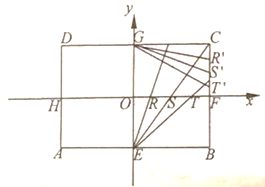
【题目】如图,矩形ABCD中,![]() ,
,![]() ,E,F,G,H分别是矩形四条边的中点,R,S,T是线段OF的四等分点,
,E,F,G,H分别是矩形四条边的中点,R,S,T是线段OF的四等分点,![]() ,
,![]() ,
,![]() 是线段CF的四等分点,分别以HF,EG为x,y轴建立直角坐标系,设ER与
是线段CF的四等分点,分别以HF,EG为x,y轴建立直角坐标系,设ER与![]() ER与
ER与![]() 分别交于
分别交于![]() ,
,![]() ,ES与
,ES与![]() ES与
ES与![]() 交于
交于![]() ,
,![]() ,ET与
,ET与![]() 交于点N,则下列关于点
交于点N,则下列关于点![]() ,
,![]() ,
,![]() ,
,![]() ,N与两个椭圆:
,N与两个椭圆:![]() :
:![]() ,
,![]() :
:![]() 的位置关系叙述正确的是( )
的位置关系叙述正确的是( )
A.三点![]() ,
,![]() ,Nspan>在
,Nspan>在![]() ,点
,点![]() 在
在![]() 上B.
上B.![]() ,
,![]() 不在
不在![]() 上,
上,![]() ,N在
,N在![]() 上
上
C.点![]() 在
在![]() 上,点
上,点![]() ,
,![]() ,
,![]() 均不在
均不在![]() 上D.
上D.![]() ,
,![]() 在
在![]() 上,
上,![]() ,
,![]() 均不在
均不在![]() 上
上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场营销人员对某商品![]() 进行市场营销调查,发现每回馈消费者一定的点数,该商品每天的销量就会发生一定的变化,经过统计得到下表:
进行市场营销调查,发现每回馈消费者一定的点数,该商品每天的销量就会发生一定的变化,经过统计得到下表:
回馈点数 | 1 | 2 | 3 | 4 | 5 |
销量(百件)/天 | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)经分析发现,可用线性回归模型拟合该商品每天的销量![]() (百件)与返还点数
(百件)与返还点数![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测若回馈6个点时该商品每天销量;
,并预测若回馈6个点时该商品每天销量;
(2)已知节日期间某地拟购买该商品的消费群体十分庞大,营销调研机构对其中的200名消费者的返点数额的心理预期值进行了抽样调查,得到如下频数表:
返还点数预期值区间 |
|
|
|
|
|
|
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
(i)求这200位拟购买该商品的消费者对返点点数的心理预期值的样本平均数及中位数的估计值(同一区间的预期值可用该区间的中点值代替;估计值精确到0.1);
(ii)将对返点点数的心理预期值在![]() 和
和![]() 的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取3名进行跟踪调查,设抽出的3人中“欲望紧缩型”消费者的人数为随机变量
的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取3名进行跟踪调查,设抽出的3人中“欲望紧缩型”消费者的人数为随机变量![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式及数据:①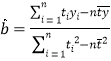 ,
,![]() ;②
;②![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 前n项和为
前n项和为![]() ,且
,且![]() 其中m为实常数,
其中m为实常数,![]() 且
且![]() .
.
(1)求证:![]() 是等比数列;
是等比数列;
(2)若数列![]() 的公比满足
的公比满足![]() 且
且![]() ,
,![]() ,求证:数列
,求证:数列![]() 是等差数列,并求
是等差数列,并求![]() 的通项公式;
的通项公式;
(3)若![]() 时,设
时,设![]() ,求数列
,求数列![]() 的前n和
的前n和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂抽取了一台设备![]() 在一段时间内生产的一批产品,测量一项质量指标值,绘制了如图所示的频率分布直方图.
在一段时间内生产的一批产品,测量一项质量指标值,绘制了如图所示的频率分布直方图.

(1)计算该样本的平均值![]() ,方差
,方差![]() ;(同一组中的数据用该组区间的中点值作代表)
;(同一组中的数据用该组区间的中点值作代表)
(2)根据长期生产经验,可以认为这台设备在正常状态下生产的产品的质量指标值服从正态分布![]() ,其中
,其中![]() 近似为样本平均值,
近似为样本平均值,![]() 近似为样本方差
近似为样本方差![]() .任取一个产品,记其质量指标值为
.任取一个产品,记其质量指标值为![]() .若
.若![]() ,则认为该产品为一等品;
,则认为该产品为一等品;![]() ,则认为该产品为二等品;若
,则认为该产品为二等品;若![]() ,则认为该产品为不合格品.已知设备
,则认为该产品为不合格品.已知设备![]() 正常状态下每天生产这种产品1000个.
正常状态下每天生产这种产品1000个.
(i)用样本估计总体,问该工厂一天生产的产品中不合格品是否超过![]() ?
?
(ii)某公司向该工厂推出以旧换新活动,补足50万元即可用设备![]() 换得生产相同产品的改进设备
换得生产相同产品的改进设备![]() .经测试,设备
.经测试,设备![]() 正常状态下每天生产产品1200个,生产的产品为一等品的概率是
正常状态下每天生产产品1200个,生产的产品为一等品的概率是![]() ,二等品的概率是
,二等品的概率是![]() ,不合格品的概率是
,不合格品的概率是![]() .若工厂生产一个一等品可获得利润50元,生产一个二等品可获得利润30元,生产一个不合格品亏损40元,试为工厂做出决策,是否需要换购设备
.若工厂生产一个一等品可获得利润50元,生产一个二等品可获得利润30元,生产一个不合格品亏损40元,试为工厂做出决策,是否需要换购设备![]() ?
?
参考数据:①![]() ;②
;②![]() ;③
;③![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1左右焦点为F1,F2直线(
1左右焦点为F1,F2直线(![]() 1)x
1)x![]() y
y![]() 0与该椭圆有一个公共点在y轴上,另一个公共点的坐标为(m,1).
0与该椭圆有一个公共点在y轴上,另一个公共点的坐标为(m,1).
(1)求椭圆C的方程;
(2)设P为椭圆C上任一点,过焦点F1,F2的弦分别为PM,PN,设![]() λ1
λ1![]() λ2
λ2![]() ,求λ1+λ2的值.
,求λ1+λ2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,将曲线
,将曲线![]() 向左平移
向左平移![]() 个单位长度得到曲线
个单位长度得到曲线![]() .
.
(1)求曲线![]() 的参数方程;
的参数方程;
(2)已知![]() 为曲线
为曲线![]() 上的动点,
上的动点, ![]() 两点的极坐标分别为
两点的极坐标分别为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com