
【题目】已知函数![]() .
.
(1)求![]() 的图像在
的图像在![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 的极大值;
的极大值;
(3)若![]() 对
对![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】(1)![]() .(2)-1;(3)
.(2)-1;(3)![]()
【解析】
(1)由函数![]() ,可得
,可得![]() ,求出
,求出![]() 和切点坐标,利用点斜式即可得出切线方程.
和切点坐标,利用点斜式即可得出切线方程.
(2)由![]() ,求得
,求得![]() ,分析
,分析![]() 在
在![]() 上单调性和零点,即可得出
上单调性和零点,即可得出![]() 单调性与极值.
单调性与极值.
(3)令![]() ,求出
,求出![]() ,对
,对![]() 分类讨论,利用导数研究其单调性即可得出实数
分类讨论,利用导数研究其单调性即可得出实数![]() 的取值范围.
的取值范围.
解:(1)因为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
因为![]() 经过
经过![]() ,
,
所以![]() 的图像在
的图像在![]() 处的切线方程为
处的切线方程为![]() ;
;
(2)因为![]() ,
,![]() ,
,
所以![]() ,
,
又![]() 在
在![]() 递减,
递减,![]() ,
,
所以在![]() ,
,![]() ,即
,即![]() 在
在![]() 递增;
递增;
在![]() ,
,![]() ,即
,即![]() 在
在![]() 递减,
递减,
所以在![]() 处,
处,![]() 取极大值,
取极大值,![]() ;
;
(3)设![]() ,
,![]() ,
,
所以![]() ,
,
①![]() 时,
时,![]() 对
对![]() 恒成立,
恒成立,
所以![]() 在
在![]() 递增,
递增,
又![]() ,
,
所以![]() 时,
时,![]() ,
,
这与![]() 对
对![]() 恒成立矛盾,舍去;
恒成立矛盾,舍去;
②![]() 时,设
时,设![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() 对
对![]() 恒成立,
恒成立,
所以![]() 在
在![]() 递减,
递减,
又![]() ,
,
所以![]() 对
对![]() 恒成立,
恒成立,
所以![]() 成立;
成立;
③![]() 时,设
时,设![]() ,
,![]() ,
,![]() ,
,
解![]() 得两根为
得两根为![]() ,
,![]() ,其中
,其中![]() ,
,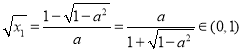 ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
所以![]() 在
在![]() 递增,
递增,
又![]() ,
,
所以![]() ,
,
这与![]() 对
对![]() 恒成立矛盾,舍去,
恒成立矛盾,舍去,
综上:![]() .
.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
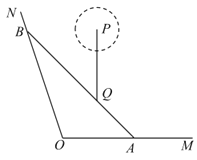
【题目】如图,![]() ,
,![]() 是某景区的两条道路(宽度忽略不计,
是某景区的两条道路(宽度忽略不计,![]() 为东西方向),Q为景区内一景点,A为道路
为东西方向),Q为景区内一景点,A为道路![]() 上一游客休息区,已知
上一游客休息区,已知![]() ,
,![]() (百米),Q到直线
(百米),Q到直线![]() ,
,![]() 的距离分别为3(百米),
的距离分别为3(百米),![]() (百米),现新修一条自A经过Q的有轨观光直路并延伸至道路
(百米),现新修一条自A经过Q的有轨观光直路并延伸至道路![]() 于点B,并在B处修建一游客休息区.
于点B,并在B处修建一游客休息区.
(1)求有轨观光直路![]() 的长;
的长;
(2)已知在景点Q的正北方6百米的P处有一大型组合音乐喷泉,喷泉表演一次的时长为9分钟,表演时,喷泉喷洒区域以P为圆心,r为半径变化,且t分钟时,![]() (百米)(
(百米)(![]() ,
,![]() ).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道
).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道![]() 以
以![]() (百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.
(百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系xOy中,圆C的参数方程为![]() (θ为参数),直线l经过定点P(2,3),倾斜角为
(θ为参数),直线l经过定点P(2,3),倾斜角为![]() .
.
(Ⅰ)写出直线l的参数方程和圆C的标准方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|PA|·|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转,如图,小卢利用图形的旋转设计某次活动的徽标,他将边长为a的正三角形ABC 绕其中心O逆时针旋转到三角形A1B1C1,且![]() .顺次连结A,A1,B,B1,C,C1,A,得到六边形徽标AA1BB1CC1 .
.顺次连结A,A1,B,B1,C,C1,A,得到六边形徽标AA1BB1CC1 .
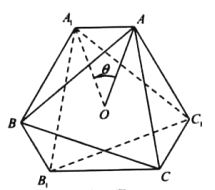
(1)当=![]() 时,求六边形徽标的面积;
时,求六边形徽标的面积;
(2)求六边形徽标的周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图①中△ABC 为直角三角形![]() D、E 分别为 AB、AC 的中点,将△ADE 沿 DE 折起使平面 ADE⊥BCED,连接 AB,AC,BE如图②所示.
D、E 分别为 AB、AC 的中点,将△ADE 沿 DE 折起使平面 ADE⊥BCED,连接 AB,AC,BE如图②所示.
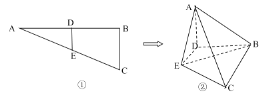
(1)在线段AC上找一点P,使EP∥平面ABD,并求出异面直线AB、EP所成的角;
(2)在平面ABD内找一点Q,使PQ⊥平面ABE,并求三棱锥P-ABE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知多面体![]() 的底面
的底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() 平面
平面![]() ,
,![]() ,且
,且![]() .
.
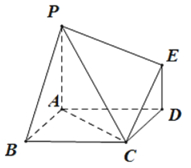
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为45°,求平面
所成的角为45°,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)满足:集合A={f(n)|n∈N*}中至少有三个不同的数成等差数列,则称函数f(x)是“等差源函数”,则下列四个函数中,“等差源函数”的个数是( )
①y=2x+1;②y=log2x;③y=2x+1;
④y=sin![]()
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com