
【题目】在锐角三角形![]() 中,
中,![]() 分别为内角
分别为内角![]() 所对的边,且满足
所对的边,且满足![]() .
.
(1)求角![]() 的大小;
的大小;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
【答案】解:(Ⅰ)因为![]() ,
,
所以![]() , ……………………………………………… 2分
, ……………………………………………… 2分
因为![]() ,所以
,所以![]() . …………………………………………………3分
. …………………………………………………3分
又![]() 为锐角,则
为锐角,则![]() . …………………………………………… 5分
. …………………………………………… 5分
(Ⅱ)由(Ⅰ)可知,![]() .因为
.因为![]() ,
,
根据余弦定理,得![]() ,………………………………………7分
,………………………………………7分
整理,得![]() .
.
由已知![]() ,则
,则![]() .
.
又![]() ,可得
,可得![]() ,
,![]() . ……………………………………… 9分
. ……………………………………… 9分
于是![]() , ………………………… 11分
, ………………………… 11分
所以![]() . …………… 13分
. …………… 13分
【解析】试题分析:(1)由正弦定理可得![]() ,即
,即![]() ,则角
,则角![]() 可求;
可求;
(2))由(1)知,![]() ,由余弦定理可得
,由余弦定理可得![]() ,进而求得
,进而求得![]() 则
则![]() 的值可求
的值可求
试题解析:(1)因为![]() ,所以
,所以![]() ,因为
,因为![]() ,
,
所以![]() ,又
,又![]() 为锐角,则
为锐角,则![]() .
.
(2)由(1)知,![]() ,因为
,因为![]() ,根据余弦定理得:
,根据余弦定理得:![]() ,整理,得
,整理,得![]() ,由已知
,由已知![]() ,则
,则![]() ,又
,又![]() ,可得
,可得![]() ,于是
,于是![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】某工厂的A、B、C三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测.
车间 | A | B | C |
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自A、B、C各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件商品来自相同车间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以原点
),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上一点,若点
上一点,若点![]() 到曲线
到曲线![]() 的最小距离为
的最小距离为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年某市政府为了有效改善市区道路交通拥堵状况出台了一系列的改善措施,其中市区公交站点重新布局和建设作为重点项目.市政府相关部门根据交通拥堵情况制订了“市区公交站点重新布局方案”,现准备对该“方案”进行调查,并根据调查结果决定是否启用该“方案”.调查人员分别在市区的各公交站点随机抽取若干市民对该“方案”进行评分,并将结果绘制成如图所示的频率分布直方图.相关规则为:①调查对象为本市市民,被调查者各自独立评分;②采用百分制评分,[60,80)内认定为满意,不低于80分认定为非常满意;③市民对公交站点布局的满意率不低于75%即可启用该“方案”;④用样本的频率代替概率.
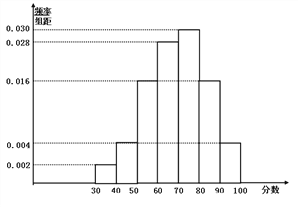
(1)从该市800万人的市民中随机抽取5人,求恰有2人非常满意该“方案”的概率;并根据所学统计学知识判断该市是否启用该“方案”,说明理由.
(2)已知在评分低于60分的被调查者中,老年人占![]() ,现从评分低于60分的被调查者中按年龄分层抽取9人以便了解不满意的原因,并从中抽取3人担任群众督查员,记
,现从评分低于60分的被调查者中按年龄分层抽取9人以便了解不满意的原因,并从中抽取3人担任群众督查员,记![]() 为群众督查员中的老人的人数,求随机变量
为群众督查员中的老人的人数,求随机变量![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中, ![]() 为坐标原点,
为坐标原点, ![]() 、
、![]() 是双曲线
是双曲线![]() 上的两个动点,动点
上的两个动点,动点![]() 满足
满足![]() ,直线
,直线![]() 与直线
与直线![]() 斜率之积为2,已知平面内存在两定点
斜率之积为2,已知平面内存在两定点![]() 、
、![]() ,使得
,使得![]() 为定值,则该定值为________
为定值,则该定值为________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校随机抽取20个班,调查各班中有网上购物经历的人数,所得数据的茎叶图如图所示.以组距为5将数据分组成[0,5),[5,10),…,[30,35),[35,40]时,所作的频率分布直方图是( )
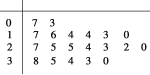

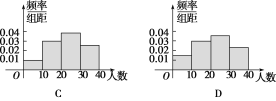
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com