
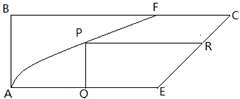
 如图,直角梯形地块ABCE,AF、EC是两条道路,其中AF是以A为顶点、AE所在直线为对称轴的抛物线的一部分,EC是线段.AB=2km,BC=6km,AE=BF=4km.计划在两条道路之间修建一个公园,
如图,直角梯形地块ABCE,AF、EC是两条道路,其中AF是以A为顶点、AE所在直线为对称轴的抛物线的一部分,EC是线段.AB=2km,BC=6km,AE=BF=4km.计划在两条道路之间修建一个公园, 解:(Ⅰ)设抛物线y2=2px
解:(Ⅰ)设抛物线y2=2px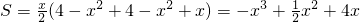 (0<x<2)
(0<x<2)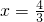
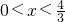 时,S'>0,∴S(x)递增;当
时,S'>0,∴S(x)递增;当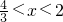 时,S'<0,∴S(x)递减;
时,S'<0,∴S(x)递减;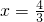 km时,
km时,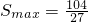 km2
km2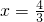 ,利用函数在(0,2)上是单峰函数,可求函数的最值.
,利用函数在(0,2)上是单峰函数,可求函数的最值.

科目:高中数学 来源: 题型:
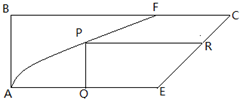 如图,直角梯形地块ABCE,AF、EC是两条道路,其中AF是以A为顶点、AE所在直线为对称轴的抛物线的一部分,EC是线段.AB=2km,BC=6km,AE=BF=4km.计划在两条道路之间修建一个公园,
如图,直角梯形地块ABCE,AF、EC是两条道路,其中AF是以A为顶点、AE所在直线为对称轴的抛物线的一部分,EC是线段.AB=2km,BC=6km,AE=BF=4km.计划在两条道路之间修建一个公园,查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在矩形地块ABCD中有两条道路AF,EC,其中AF是以A为顶点的抛物线段,EC是线段.AB=2km,BC=6km,AE=BF=4km.在两条道路之间计划修建一个花圃,花圃形状为直角梯形QPRE(线段EQ和RP为两个底边,如图所示).求该花圃的最大面积.
如图,在矩形地块ABCD中有两条道路AF,EC,其中AF是以A为顶点的抛物线段,EC是线段.AB=2km,BC=6km,AE=BF=4km.在两条道路之间计划修建一个花圃,花圃形状为直角梯形QPRE(线段EQ和RP为两个底边,如图所示).求该花圃的最大面积.查看答案和解析>>
科目:高中数学 来源:2012届江苏省高二下学期期末考试数学(理)试卷 题型:解答题
如图,在矩形地块ABCD中有两条道路AF,EC,其中AF是以A为顶点的抛物线段,EC是线段.AB=2km,BC=6km,AE=BF=4km.在两条道路之间计划修建一个花圃,花圃形状为直角梯形QPRE(线段EQ和RP为两个底边,如图所示).求该花圃的最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在矩形地块ABCD中有两条道路AF,EC,其中AF是以A为顶点的抛物线段,EC是线段.AB=2km,BC=6km,AE=BF=4km.在两条道路之间计划修建一个花圃,花圃形状为直角梯形QPRE(线段EQ和RP为两个底边,如图所示).求该花圃的最大面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com