
【题目】在边长为2的等边三角形![]() 中,点
中,点![]() 分别是边
分别是边![]() 上的点,满足
上的点,满足![]() 且
且![]() ,(
,(![]() ),将
),将![]() 沿直线
沿直线![]() 折到
折到![]() 的位置.在翻折过程中,下列结论不成立的是( )
的位置.在翻折过程中,下列结论不成立的是( )
A.在边![]() 上存在点
上存在点![]() ,使得在翻折过程中,满足
,使得在翻折过程中,满足![]() 平面
平面![]()
B.存在![]() ,使得在翻折过程中的某个位置,满足平面
,使得在翻折过程中的某个位置,满足平面![]() 平面
平面![]()
C.若![]() ,当二面角
,当二面角![]() 为直二面角时,
为直二面角时,![]()
D.在翻折过程中,四棱锥![]() 体积的最大值记为
体积的最大值记为![]() ,
,![]() 的最大值为
的最大值为![]()
【答案】ABC
【解析】
对于A.在边![]() 上点F,在
上点F,在![]() 上取一点N,使得
上取一点N,使得![]() ,在
,在![]() 上取一点H,使得
上取一点H,使得![]() ,作
,作![]() 交
交![]() 于点G,即可判断出结论.
于点G,即可判断出结论.
对于B,![]() ,在翻折过程中,点
,在翻折过程中,点![]() 在底面
在底面![]() 的射影不可能在交线
的射影不可能在交线![]() 上,即可判断出结论.
上,即可判断出结论.
对于C,![]() ,当二面角
,当二面角![]() 为直二面角时,取ED的中点M,可得
为直二面角时,取ED的中点M,可得![]() 平面
平面![]() .可得
.可得![]() ,结合余弦定理即可得出.
,结合余弦定理即可得出.
对于D.在翻折过程中,取平面![]() 平面
平面![]() ,四棱锥
,四棱锥![]() 体积
体积![]() ,
,![]() ,利用导数研究函数的单调性即可得出.
,利用导数研究函数的单调性即可得出.
对于A.在边![]() 上点F,在
上点F,在![]() 上取一点N,使得
上取一点N,使得![]() ,在
,在![]() 上取一点H,使得
上取一点H,使得![]() ,作
,作![]() 交
交![]() 于点G,如图所示,
于点G,如图所示,

则可得![]() 平行且等于
平行且等于![]() ,即四边形
,即四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,而
,而![]() 始终与平面
始终与平面![]() 相交,
相交,
因此在边![]() 上不存在点F,使得在翻折过程中,满足
上不存在点F,使得在翻折过程中,满足![]() 平面
平面![]() ,A不正确.
,A不正确.
对于B,![]() ,在翻折过程中,点
,在翻折过程中,点![]() 在底面
在底面![]() 的射影不可能在交线
的射影不可能在交线![]() 上,因此不满足平面
上,因此不满足平面![]() 平面
平面![]() ,因此B不正确.
,因此B不正确.
对于C.![]() ,当二面角
,当二面角![]() 为直二面角时,取
为直二面角时,取![]() 的中点M,如图所示:
的中点M,如图所示:

可得![]() 平面
平面![]() ,
,
则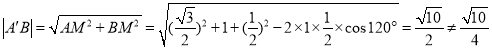 ,因此C不正确;
,因此C不正确;
对于D.在翻折过程中,取平面AED⊥平面BCDE,四棱锥![]() 体积
体积![]() ,
,![]() ,
,![]() ,可得
,可得![]() 时,函数
时,函数![]() 取得最大值
取得最大值![]() ,因此D正确.
,因此D正确.
综上所述,不成立的为ABC.
故选:ABC.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,北京2022年冬奥组委会启动志愿者全球招募,仅一个月内报名人数便突破60万,其中青年学生约有50万人.现从这50万青年学生志愿者中,按男女分层抽样随机选取20人进行英语水平测试,所得成绩(单位:分)统计结果用茎叶图记录如下:
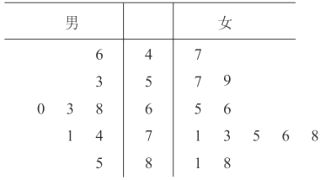
(Ⅰ)试估计在这50万青年学生志愿者中,英语测试成绩在80分以上的女生人数;
(Ⅱ)从选出的8名男生中随机抽取2人,记其中测试成绩在70分以上的人数为X,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)为便于联络,现将所有的青年学生志愿者随机分成若干组(每组人数不少于5000),并在每组中随机选取![]() 个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出
个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出![]() 的最小值.(结论不要求证明)
的最小值.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某物流公司专营从甲地到乙地的货运业务(货物全部用统一规格的包装箱包装),现统计了最近100天内每天可配送的货物量,按照可配送货物量T(单位:箱)分成了以下几组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并绘制了如图所示的频率分布直方图(同一组数据用该组数据的区间中点值作代表,将频率视为概率).
,并绘制了如图所示的频率分布直方图(同一组数据用该组数据的区间中点值作代表,将频率视为概率).
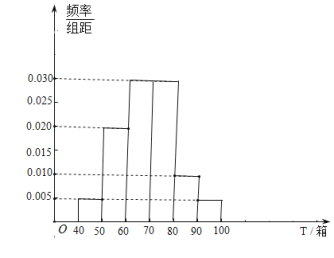
(1)该物流公司负责人决定用分层抽样的方法从前3组中随机抽出11天的数据来分析可配送货物量少的原因,并从这11天的数据中再抽出3天的数据进行财务分析,求这3天的数据中至少有2天的数据来自![]() 这一组的概率.
这一组的概率.
(2)由频率分布直方图可以认为,该物流公司每日的可配送货物量T(单位:箱)服从正态分布![]() ,其中
,其中![]() 近似为样本平均数.
近似为样本平均数.
(ⅰ)试利用该正态分布,估计该物流公司2000天内日货物配送量在区间![]() 内的天数(结果保留整数).
内的天数(结果保留整数).
(ⅱ)该物流公司负责人根据每日的可配送货物量为公司装卸货物的员工制定了两种不同的工作奖励方案.
方案一:直接发放奖金,按每日的可配送货物量划分为以下三级:![]() 时,奖励50元;
时,奖励50元;![]() ,奖励80元;
,奖励80元;![]() 时,奖励120元.
时,奖励120元.
方案二:利用抽奖的方式获得奖金,其中每日的可配送货物量不低于![]() 时有两次抽奖机会,每日的可配送货物量低于
时有两次抽奖机会,每日的可配送货物量低于![]() 时只有一次抽奖机会,每次抽奖的奖金及对应的概率分别为
时只有一次抽奖机会,每次抽奖的奖金及对应的概率分别为
奖金 | 50 | 100 |
概率 |
|
|
小张恰好为该公司装卸货物的一名员工,试从数学期望的角度分析,小张选择哪种奖励方案对他更有利?
附:若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() 为
为![]() 中点,下列说法中
中点,下列说法中
(1)![]() ;
;
(2)记二面角![]() 的平面角分别为
的平面角分别为![]() ;
;
(3)记![]() 的面积分别为
的面积分别为![]() ;
;
(4)![]() ,
,
正确说法的个数为( )

A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ?如果存在,求
?如果存在,求![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com