
【题目】从某食品厂生产的面包中抽取![]() 个,测量这些面包的一项质量指标值,由测量结果得如下频数分布表:
个,测量这些面包的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 |
|
|
|
|
|
频数 |
|
|
|
|
|

(1)在相应位置上作出这些数据的频率分布直方图;
(2)估计这种面包质量指标值的平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(3)根据以上抽样调查数据,能否认为该食品厂生产的这种面包符合“质量指标值不低于![]() 的面包至少要占全部面包
的面包至少要占全部面包![]() 的规定?”
的规定?”
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
:![]() ,点
,点![]() .
.
(1)求点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 的坐标;
的坐标;
(2)直线![]() 关于点
关于点![]() 对称的直线
对称的直线![]() 的方程;
的方程;
(3)以![]() 为圆心,3为半径长作圆,直线
为圆心,3为半径长作圆,直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某幼儿园雏鹰班的生活老师统计2018年上半年每个月的20日的昼夜温差![]() ,
,![]() 和患感冒的小朋友人数(
和患感冒的小朋友人数(![]() /人)的数据如下:
/人)的数据如下:
温差 |
|
|
|
|
|
|
患感冒人数 | 8 | 11 | 14 | 20 | 23 | 26 |
其中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)请用相关系数加以说明是否可用线性回归模型拟合![]() 与
与![]() 的关系;
的关系;
(Ⅱ)建立![]() 关于
关于![]() 的回归方程(精确到
的回归方程(精确到![]() ),预测当昼夜温差升高
),预测当昼夜温差升高![]() 时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
参考数据:![]() .参考公式:相关系数:
.参考公式:相关系数: ,回归直线方程是
,回归直线方程是![]() ,
, ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费用支出![]() 与销售额
与销售额![]() 之间有如下的对应数据:
之间有如下的对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为10时,销售收入![]() 的值.
的值.
参考公式及数据: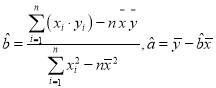
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 在同一个周期内,当
在同一个周期内,当![]() 时y取最大值1,当
时y取最大值1,当![]() 时,y取最小值﹣1.
时,y取最小值﹣1.
(1)求函数的解析式y=f(x);
(2)函数y=sinx的图象经过怎样的变换可得到y=f(x)的图象?
(3)若函数f(x)满足方程f(x)=a(0<a<1),求在[0,2π]内的所有实数根之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
(1)请在图中画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测记忆力为9的同学的判断力.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形(记为Q).
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P是直线x=﹣4与x轴的交点,过点P的直线l与椭圆C相交于M,N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线l斜率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com