
【题目】已知函数![]() ,下列结论中不正确的是( )
,下列结论中不正确的是( )
A. ![]() 的图象关于点
的图象关于点![]() 中心对称
中心对称
B. ![]() 的图象关于直线
的图象关于直线![]() 对称
对称
C. ![]() 的最大值为
的最大值为![]()
D. ![]() 既是奇函数,又是周期函数
既是奇函数,又是周期函数
【答案】C
【解析】试题分析:对于A中,因为![]() ,
,
则![]() ,所以
,所以![]() ,可得
,可得![]() 的图象关于
的图象关于![]() 中心对称,故A正确;对于B,因为
中心对称,故A正确;对于B,因为![]()
![]() ,
,![]() ,所以
,所以![]() ,可得
,可得![]() 的图象关于
的图象关于![]() 中心对称,故B正确;对于C,化简得
中心对称,故B正确;对于C,化简得![]()
![]() ,令
,令![]() ,因为
,因为![]() 的导数
的导数
![]() ,所以当
,所以当![]() 或
或![]() 时,
时,![]() ,函数
,函数![]() 为减函数;当
为减函数;当![]() 时,
时,![]() ,函数
,函数![]() 为增函数,因此函数
为增函数,因此函数![]() 的最大值为
的最大值为![]() 或
或![]() 时的函数值,结合
时的函数值,结合![]() ,可得
,可得![]() 的最大值为
的最大值为![]() ,由此可得
,由此可得![]() 的最大值为
的最大值为![]() ,而不是
,而不是![]() ,所以不正确;对于D,因为
,所以不正确;对于D,因为![]() ,所以
,所以![]() 是奇函数,因为
是奇函数,因为![]() ,所以
,所以![]() 为函数的一个周期,得
为函数的一个周期,得![]() 为周期,可得
为周期,可得![]() 既是奇函数,又是周期函数,所以正确,故选D.
既是奇函数,又是周期函数,所以正确,故选D.
【方法点晴】本题主要考查了三角函数的图象与性质及三角函数的最值问题,其中解答中涉及到三角函数的解析式、三角函数的奇偶性、三角函数的单调性和周期性等知识点的综合考查,着重考查了三角恒等变换公式、利用导数研究函数的单调性和函数的图象的对称性等知识,体现了分析问题和解答问题的能力,属于中档试题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+3x2﹣9x+m
(1)求函数f(x)=x3+3x2﹣9x+m的单调递增区间;
(2)若函数f(x)在区间[0,2]上的最大值12,求函数f(x)在该区间上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,PA⊥底面ABCD,AB⊥AC,AB=1,BC=2,PA= ![]() ,E为BC的中点.
,E为BC的中点. 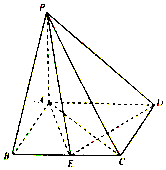
(1)证明:PE⊥ED;
(2)求二面角E﹣PD﹣A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若在曲线f(x,y)=0(或y=f(x))上两个不同点处的切线重合,则称这条切线为曲线f(x,y)=0或y=f(x)的“自公切线”.下列方程:
①x2﹣y2=1;
②y=x2﹣|x|;
③y=3sinx+4cosx;
④|x|+1= ![]()
对应的曲线中存在“自公切线”的有( )
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的参数方程为:
的参数方程为: 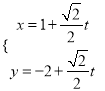 ,曲线
,曲线![]() 的极坐标方程:
的极坐标方程: ![]()
(1)写出![]() 和
和![]() 的普通方程;
的普通方程;
(2)若![]() 与
与![]() 交于两点
交于两点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值;
的距离的最大值;
(2)若曲线![]() 上的所有点都在直线
上的所有点都在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B两地的距离是120km,按交通法规规定,A,B两地之间的公路车速应限制在50~100km/h,假设汽油的价格是6元/升,以xkm/h速度行驶时,汽车的耗油率为 ![]() ,司机每小时的工资是36元,那么最经济的车速是多少?如果不考虑其他费用,这次行车的总费用是多少?
,司机每小时的工资是36元,那么最经济的车速是多少?如果不考虑其他费用,这次行车的总费用是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一元二次不等式﹣x2+x+2>0的解集是( )
A.{x|x<﹣1或x>2}
B.{x|x<﹣2或x>1}
C.{x|﹣1<x<2}
D.{x|﹣2<x<1}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com