
【题目】已知函数![]() (
(![]() 且
且![]() 为常数).
为常数).
(1)当![]() 时,讨论函数
时,讨论函数![]() 在
在![]() 的单调性;
的单调性;
(2)设![]() 可求导数,且它的导函数
可求导数,且它的导函数![]() 仍可求导数,则
仍可求导数,则![]() 再次求导所得函数称为原函数
再次求导所得函数称为原函数![]() 的二阶函数,记为
的二阶函数,记为![]() ,利用二阶导函数可以判断一个函数的凹凸性.一个二阶可导的函数在区间
,利用二阶导函数可以判断一个函数的凹凸性.一个二阶可导的函数在区间![]() 上是凸函数的充要条件是这个函数在
上是凸函数的充要条件是这个函数在![]() 的二阶导函数非负.
的二阶导函数非负.
若![]() 在
在![]() 不是凸函数,求
不是凸函数,求![]() 的取值范围.
的取值范围.
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 中,
中, ![]() 为正三角形,
为正三角形, ![]() ,
, ![]() ,
, ![]() 与
与![]() 中心
中心![]() 点,将
点,将![]() 沿边
沿边![]() 折起,使
折起,使![]() 点至
点至![]() 点,已知
点,已知![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
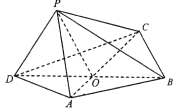
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求已知二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品.为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如下表所示:
,如下表所示:

已知![]() .
.
(1)求出![]() 的值;
的值;
(2)已知变量![]() ,
, ![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (件)关于试销单价
(件)关于试销单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;
;
(3)用![]() 表示用正确的线性回归方程得到的与
表示用正确的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 的残差的绝对值
的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从6个销售数据中任取2个,求抽取的2个销售数据中至少有1个是“好数据”的概率.
称为一个“好数据”.现从6个销售数据中任取2个,求抽取的2个销售数据中至少有1个是“好数据”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 关于直线
关于直线![]() 对称的圆为
对称的圆为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与圆
与圆![]() 交于
交于![]() 两点,
两点, ![]() 是坐标原点,是否存在这样的直线
是坐标原点,是否存在这样的直线![]() ,使得在平行四边形
,使得在平行四边形![]() 中
中![]() ?若存在,求出所有满足条件的直线
?若存在,求出所有满足条件的直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甘肃省瓜州县自古就以盛产“美瓜”而名扬中外,生产的“瓜州蜜瓜”有4个系列30多个品种,质脆汁多,香甜可口,清爽宜人,含糖量达14%-19%,是消暑止渴的佳品,有诗赞曰:冰泉浸绿玉,霸刀破黄金;凉冷消晚署,清甘洗渴心,调查表明,蜜瓜的甜度与海拔高度、日照时长、温差有极强的相关性,分别用![]() 表示蜜瓜甜度与海拔高度、日照时长、温差的相关程度,并对它们进行量化:0表示一般,1表示良,2表示优,再用综合指标
表示蜜瓜甜度与海拔高度、日照时长、温差的相关程度,并对它们进行量化:0表示一般,1表示良,2表示优,再用综合指标![]() 的值评定蜜瓜的等级,若
的值评定蜜瓜的等级,若![]() ,则为一级;若
,则为一级;若![]() ,则为二级;若
,则为二级;若![]() ,则为三级.近年来,周边各省也开始发展蜜瓜种植,为了了解目前蜜瓜在周边各省的种植情况,研究人员从不同省份随机抽取了10块蜜瓜种植地,得到如下结果:
,则为三级.近年来,周边各省也开始发展蜜瓜种植,为了了解目前蜜瓜在周边各省的种植情况,研究人员从不同省份随机抽取了10块蜜瓜种植地,得到如下结果:

(1)若有蜜瓜种植地110块,试估计等级为一级的蜜瓜种植地的数量;
(2)在所取样本的二级和三级蜜瓜种植地中任取2块, ![]() 表示取到三级蜜瓜种植地的数量,求随机变量
表示取到三级蜜瓜种植地的数量,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 分别到两定点
分别到两定点![]()
![]() 连线的斜率之乘积为
连线的斜率之乘积为![]() ,设
,设![]() 的轨迹为曲线
的轨迹为曲线![]() ,
, ![]() ,
, ![]() 分别为曲线
分别为曲线![]() 的左右焦点,则下列命题中:
的左右焦点,则下列命题中:
(1)曲线![]() 的焦点坐标为
的焦点坐标为![]() ,
, ![]() ;
;
(2)若![]() ,则
,则![]()
![]() ;
;
(3)当![]() 时,
时, ![]() 的内切圆圆心在直线
的内切圆圆心在直线![]() 上;
上;
(4)设![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某微信群中有甲、乙、丙、丁、戊五个人玩抢红包游戏,现有4个红包,每人最多抢一个,且红包被全部抢完,4个红包中有2个6元,1个8元,1个10元(红包中金额相同视为相同红包),则甲、乙都抢到红包的情况有( )
A. 18种 B. 24种 C. 36种 D. 48种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin(2x+
sin(2x+ ![]() ),给出下列四个命题:
),给出下列四个命题:
①函数f(x)在区间[ ![]() ,
, ![]() ]上是减函数;
]上是减函数;
②直线x= ![]() 是f(x)的图象的一条对称轴;
是f(x)的图象的一条对称轴;
③函数f(x)的图象可以由函数y= ![]() sin2x的图象向左平移
sin2x的图象向左平移 ![]() 而得到;
而得到;
④函数f(x)的图象的一个对称中心是( ![]() ,0).
,0).
其中正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差d>0.设{an}的前n项和为Sn,a1=1,S2·S3=36.
(1)求d及Sn;
(2)求m,k(m,k∈N*)的值,使得am+am+1+am+2+…+am+k=65.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com