
分析 先将问题等价为:f'(x)≥0在x∈(-∞,-$\frac{3}{2}$)上恒成立,再通过分离参数发求a的取值范围.
解答 解:根据题意,问题等价为:
f'(x)≥0在x∈(-∞,-$\frac{3}{2}$)上恒成立,
即x2+2x+a≥0恒成立,
分离参数a得,a≥-x2-2x=-(x+1)2+1,
所以,a≥[-(x+1)2+1]max=$\frac{3}{4}$,
仅当x=-$\frac{3}{2}$时,上式取得最大值,
所以,实数a的取值范围为:[$\frac{3}{4}$,+∞).
点评 本题主要考查了运用导数研究函数的单调性和确定函数的单调区间,涉及不等式恒成立问题的解法,属于基础题.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 处罚金额x(单位:元) | 0 | 5 | 10 | 15 | 20 |
| 会闯红灯的人数y | 80 | 50 | 40 | 20 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
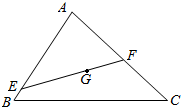 如图,G是△ABC的重心,过G的直线与边AB,AC分别相交于点E,F,若AE=mAB,AF=nAC(mn≠0),求$\frac{1}{m}$+$\frac{1}{n}$的值.
如图,G是△ABC的重心,过G的直线与边AB,AC分别相交于点E,F,若AE=mAB,AF=nAC(mn≠0),求$\frac{1}{m}$+$\frac{1}{n}$的值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 1+$\frac{1}{2}$ | C. | 1+$\frac{1}{2}$+$\frac{1}{3}$ | D. | 1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com