
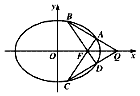
 如图,过椭圆M:$\frac{{x}^{2}}{2}$+y2=1的右焦点F作直线交椭圆于A,C两点.
如图,过椭圆M:$\frac{{x}^{2}}{2}$+y2=1的右焦点F作直线交椭圆于A,C两点.分析 (1)设A(x1,y1),C(x2,y2),Q(q,0),当A,C不在x轴上时,设直线AC的方程为:x=ty+1,代入椭圆M的方程可得:(2+t2)y2+2ty-1=0.由题知,kAQ+kCQ=0,利用斜率计算公式化简即可得出.
(2)由(1)知,∠AQF=∠CQF,∠BQF=∠DQF,所以B,C关于x轴对称,A,D关于x轴对称.所以四边形ABCD是一个等腰梯形,则四边形ABCD的面积S=|x1-x2|•|y1-y2|=|t|•$|{y}_{1}-{y}_{2}{|}^{2}$=$\frac{8({t}^{2}+1)|t|}{({t}^{2}+2)^{2}}$.由对称性不妨设t>0,利用导数研究其单调性即可得出.
解答 解:(1)设A(x1,y1),C(x2,y2),Q(q,0),
当A,C不在x轴上时,设直线AC的方程为:x=ty+1,
代入椭圆M的方程可得:(2+t2)y2+2ty-1=0.
则y1+y2=-$\frac{2t}{2+{t}^{2}}$,y1•y2=-$\frac{1}{2+{t}^{2}}$,
由题知,kAQ+kCQ=$\frac{{y}_{1}}{{x}_{1}-q}$+$\frac{{y}_{2}}{{x}_{2}-q}$=$\frac{{y}_{1}({x}_{2}-q)+{y}_{2}({x}_{1}-q)}{({x}_{1}-q)({x}_{2}-q)}$=$\frac{{y}_{1}(t{y}_{2}+1-q)+{y}_{2}(t{y}_{1}+1-q)}{({x}_{1}-q)({x}_{2}-q)}$=$\frac{2t{y}_{1}{y}_{2}+(1-q)({y}_{1}+{y}_{2})}{({x}_{1}-q)({x}_{2}-q)}$=0,
即2ty1•y2+(1-q)(y1+y2)=0,∴2t•(-$\frac{1}{2+{t}^{2}}$)+(1-q)•(-$\frac{2t}{2+{t}^{2}}$)=0,
化为:-2t-2t(1-q)=0,
由题知无论t取何值,上式恒成立,则q=2,
当A,C在x轴上时,定点Q(2,0)依然可使∠AQF=∠CQF成立,
所以点Q的坐标是(2,0).
(2)由(1)知,∠AQF=∠CQF,∠BQF=∠DQF,
所以B,C关于x轴对称,A,D关于x轴对称.
所以四边形ABCD是一个等腰梯形,
则四边形ABCD的面积S=|x1-x2|•|y1-y2|=|t|•$|{y}_{1}-{y}_{2}{|}^{2}$=$\frac{8({t}^{2}+1)|t|}{({t}^{2}+2)^{2}}$.
由对称性不妨设t>0,
求导可得:S′=-8•$\frac{({t}^{4}-3{t}^{2}-2)}{({t}^{2}+2)^{3}}$,
令S′=0,可得t2=$\frac{3+\sqrt{17}}{2}$.
由于S(t)在$(0,\sqrt{\frac{3+\sqrt{17}}{2}})$上单调递增,在$(\sqrt{\frac{3+\sqrt{17}}{2}},+∞)$上单调递减,
所以当t2=$\frac{3+\sqrt{17}}{2}$时,四边形ABCD的面积S取得最大值.
此时,直线AC的方程是:x=$±\sqrt{\frac{3+\sqrt{17}}{2}}$y+1.
点评 本题考查了直线与椭圆相交问题、一元二次方程的根与系数的关系、利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 在四棱锥S-ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2$\sqrt{3}$,BA=BS=4.
在四棱锥S-ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2$\sqrt{3}$,BA=BS=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分不用必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $2\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若m>0,则方程x2+x-m=0有实数根”的逆否命题为:“若方程x2+x-m=0无实数根,则m≤0”. | |
| B. | 对于命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,均有x2+x+1≥0. | |
| C. | 若p∧q为假命题,则p,q中至少一个为假命题. | |
| D. | “$θ=2kπ+\frac{π}{6}$”是“$sinθ=\frac{1}{2}$”的充要条件. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com