

 解:过AD做底面ABCD垂直的平面交EF于G点
解:过AD做底面ABCD垂直的平面交EF于G点 ,GH=1
,GH=1
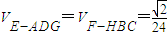 ,
,
 =
=



 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:单元双测 同步达标活页试卷 高二数学(下A) 人教版 题型:013
如图所示,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF∥AB,EF=![]() ,EF与面AC的距离为2,则该多面体的体积为
,EF与面AC的距离为2,则该多面体的体积为

A.![]()
B.5
C.6
D.![]()
查看答案和解析>>
科目:高中数学 来源:全优设计必修二数学苏教版 苏教版 题型:044
正方体是常见并且重要的多面体,对它的研究将有助于我们对立体几何一些概念的理解和掌握.如图所示,在正方体AC1中,E、F、G、H分别是所在棱的中点,请思考并回答下列问题:

(1)点E、F、G、H共面吗?
(2)直线EF、GH、DG能交于一点吗?
(3)若E、F、G、H四点共面,怎样才能画出过四点E、F、G、H的平面与正方体的截面?
(4)若正方形的棱长为a,那么(3)中的截面面积是多少?
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:013
如图所示,在多面体ABCDEF中,已知ABCD是边长为3的正方形,EF∥AB, ,EF与面AC的距离为2,则该多面体的体积为
,EF与面AC的距离为2,则该多面体的体积为

[ ]


查看答案和解析>>
科目:高中数学 来源: 题型:013
如图所示,在多面体
ABCDEF中,已知ABCD是边长为3的正方形,EF∥AB, ,EF与面AC的距离为2,则该多面体的体积为
,EF与面AC的距离为2,则该多面体的体积为

[
]|
A . |
B .5 |
C .6 |
D . |
查看答案和解析>>
科目:高中数学 来源:同步题 题型:单选题
 ,BB1=BC=6,E、F为侧棱AA1上的两点,且EF=3,则多面体BB1C1CEF的体积为
,BB1=BC=6,E、F为侧棱AA1上的两点,且EF=3,则多面体BB1C1CEF的体积为
[ ]
A.30
B.18
C.15
D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com