
【题目】某商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客购物的相关数据如下表:
位顾客购物的相关数据如下表:
一次购物款(单位:元) |
|
|
|
|
|
顾客人数 |
|
|
|
|
|
统计结果显示![]() 位顾客中购物款不低于
位顾客中购物款不低于![]() 元的顾客占
元的顾客占![]() ,该商场每日大约有
,该商场每日大约有![]() 名顾客,为了增加商场销售额度,对一次购物不低于
名顾客,为了增加商场销售额度,对一次购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(Ⅰ)试确定![]() ,
, ![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(Ⅱ)现有![]() 人前去该商场购物,求获得纪念品的数量
人前去该商场购物,求获得纪念品的数量![]() 的分布列与数学期望.
的分布列与数学期望.
 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
【题目】某市县乡教师流失现象非常严重,为了县乡孩子们能接受良好教育,某市今年要为两所县乡中学招聘储备未来三年的教师,已知现在该市县乡中学无多余教师,为决策应招聘多少县乡教师搜集并整理了该市50所县乡中学在过去三年内的教师流失数,得到如表的频率分布表:以这50所县乡中学流失教师数的频率代替一所县乡中学流失教师数发生的概率.
(1)求该市所有县乡中学教师流失数不低于8的概率;
(2)若从上述50所县乡中学中流失教师数不低于9的县乡学校中任取两所调查回访,了解其中原因,求这两所学校的教师流失数都是10的概率.
流失教师数 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
频数 | 2 | 4 | 11 | 16 | 12 | 3 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的首项为
的首项为![]() ,前
,前![]() 项和为
项和为![]() ,若对任意的
,若对任意的![]() ,均有
,均有![]() (
(![]() 是常数且
是常数且![]() )成立,则称数列
)成立,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)若数列![]() 为“
为“![]() 数列”,求数列
数列”,求数列![]() 的通项公式;
的通项公式;
(2)是否存在数列![]() 既是“
既是“![]() 数列”,也是“
数列”,也是“![]() 数列”?若存在,求出符合条件的数列
数列”?若存在,求出符合条件的数列![]() 的通项公式及对应的
的通项公式及对应的![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)若数列![]() 为“
为“![]() 数列”,
数列”, ![]() ,设
,设![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018天一大联考高中毕业班阶段性测试(四)】已知函数![]() ,
, ![]() .
.
(I)若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(II)证明:对于任意正整数![]() ,都有
,都有![]() 成立.
成立.
附: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
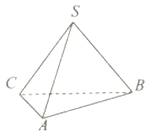
【题目】三棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
, ![]() 是等腰直角三角形
是等腰直角三角形![]() 的斜边,且
的斜边,且![]() .
.
(1)求证: ![]() ;
;
(2)已知平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,且
,且![]() 到平面
到平面![]() 的距离相等,试确定直线
的距离相等,试确定直线![]() 及点
及点![]() 的位置(说明作法及理由),并求三棱锥
的位置(说明作法及理由),并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com