
【题目】甲,乙两人玩摸球游戏,每两局为一轮,每局游戏的规则如下:甲,乙两人均从装有4只红球、1只黑球的袋中轮流不放回摸取1只球,摸到黑球的人获胜,并结束该局.
(1)若在一局中甲先摸,求甲在该局获胜的概率;
(2)若在一轮游戏中约定:第一局甲先摸,第二局乙先摸,每一局先摸并获胜的人得1分,后摸井获胜的人得2分,未获胜的人得0分,求此轮游戏中甲得分X的概率分布及数学期望.
 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】为节能环保,推进新能源汽车推广和应用,对购买纯电动汽车的用户进行财政补贴. 某地补贴政策如下(![]() 表示纯电续航里程):
表示纯电续航里程):
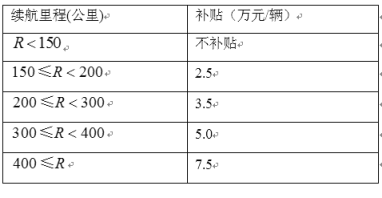
有![]() 三个纯电动汽车4s店分别销售不同品牌的纯电动汽车,在一个月内它们的销售情况如下: (每位客户只能购买一辆纯电动汽车)
三个纯电动汽车4s店分别销售不同品牌的纯电动汽车,在一个月内它们的销售情况如下: (每位客户只能购买一辆纯电动汽车)

(Ⅰ)从上述购买纯电动汽车的客户中随机选一人,求此人购买的是![]() 店纯电动汽车且享受补贴不低于3.5万元的概率;
店纯电动汽车且享受补贴不低于3.5万元的概率;
(Ⅱ)从购买![]() 店纯电动汽车的客户中按分层抽样的方法随机选6人,再从这6人中随机选2人,进行使用满意度的调查,求这两人享受补贴恰好相同的概率;
店纯电动汽车的客户中按分层抽样的方法随机选6人,再从这6人中随机选2人,进行使用满意度的调查,求这两人享受补贴恰好相同的概率;
(Ⅲ)分别用![]() 表示购买
表示购买![]() 店和
店和![]() 店纯电动汽车客户享受补贴的平均值,比较
店纯电动汽车客户享受补贴的平均值,比较![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究变量![]() 得到一组样本数据,进行回归分析,有以下结论
得到一组样本数据,进行回归分析,有以下结论
①残差图中残差点所在的水平带状区域越窄,则回归方程的预报精确度越高;
②用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小说明拟合效果越好;
越小说明拟合效果越好;
③在回归直线方程![]() 中,当变量
中,当变量![]() 每增加1个单位时,变量
每增加1个单位时,变量![]() 就增加2个单位
就增加2个单位
④若变量![]() 和
和![]() 之间的相关系数为
之间的相关系数为![]() ,则变量
,则变量![]() 和
和![]() 之间的负相关很强
之间的负相关很强
以上正确说法的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A是椭圆![]() 的左顶点,点P,Q在椭圆上且均在x轴上方.
的左顶点,点P,Q在椭圆上且均在x轴上方.
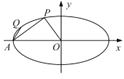
(1)若直线AP与OP垂直,求点P的坐标;
(2)若直线AP,AQ的斜率之积为![]() ,求直线PQ的斜率的取值范围.
,求直线PQ的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表:
列联表:
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)判断能否有![]() 的把握认为是否生二孩与头胎的男女情况有关;附:
的把握认为是否生二孩与头胎的男女情况有关;附:
| 0,15 | 0.05 | 0.01 | 0.0012.0 |
k | 2.072 | 3.841 | 6.635 | 10.828 |
 (其中
(其中![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据以往的经验,某工程施工期间的降水量![]() (单位:
(单位:![]() )对工期的影响如下表:
)对工期的影响如下表:
降水量 |
|
|
|
|
工期延误天数 |
|
|
|
|
历年气象资料表明,该工程施工期间降水量![]() 小于
小于![]() 、
、![]() 、
、![]() 的概率分别为
的概率分别为![]() 、
、![]() 、
、![]() ,求:
,求:
(1)在降水量![]() 至少是
至少是![]() 的条件下,工期延误不超过
的条件下,工期延误不超过![]() 天的概率;
天的概率;
(2)工期延误天数![]() 的均值与方差.
的均值与方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人民生活水平的提高,对城市空气质量的关注度也逐步增大,图2是某城市1月至8月的空气质量检测情况,图中一、二、三、四级是空气质量等级, 一级空气质量最好,一级和二级都是质量合格天气,下面四种说法正确的是( )
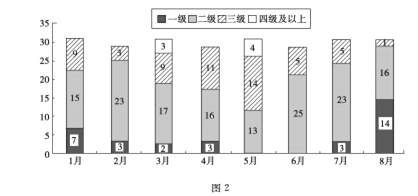
①1月至8月空气合格天数超过20天的月份有5个
②第二季度与第一季度相比,空气达标天数的比重下降了
③8月是空气质量最好的一个月
④6月份的空气质量最差
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com