
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
���� ��1�����������Ķ�����д�ɶ�Ӧ�ĵ�����꣬������ϵ����������õ�ɢ��ͼ��
��2������������������������ع鷽�̵�ϵ�����õ����Իع鷽�̣�
��3���������Իع鷽�̣�����x=100ʱ�������ܺģ�����ȼ���ǰ���͵ı�ú��
��� �⣺��1�����������Ķ�����д�ɶ�Ӧ�ĵ�����꣬
������ϵ����������õ�ɢ��ͼ���£�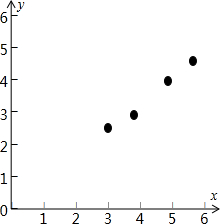
��2���ɶ������ݣ������
$\overline{x}$=$\frac{1}{4}$����3+4+5+6��=4.5��
$\overline{y}$=$\frac{1}{4}$����2.5+3+4+4.5��=3.5��
$\sum_{i=1}^{4}$${{x}_{i}}^{2}$=32+42+52+62=86��
$\sum_{i=1}^{4}$xiyi=3��2.5+4��3+5��4+6��4.5=66.5��
��ع鷽�̵�ϵ��Ϊ$\widehat{b}$=$\frac{66.5-4��4.5��3.5}{86-4{��4.5}^{2}}$=0.7��
$\widehat{a}$=3.5-0.7��4.5=0.35��
���������Իع鷽��Ϊ$\widehat{y}$=0.7x+0.35��
��3���ɣ�2�������Իع鷽�̣���������100�ּײ�Ʒ�������ܺ�Ϊ
0.7��100+0.35=70.35���֣���
��90-70.35=19.65�֣�
Ԥ��ȼ���ǰ������19.65�ֱ�ú��
���� ���⿼����ɢ��ͼ�����Իع鷽�̵�Ӧ�����⣬�ǻ�����Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��n | B�� | m��n | C�� | m��n | D�� | m��n |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | b��a��c | C�� | a��c��b | D�� | c��a��b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $y=\sqrt{x^2}$��$y=\root{3}{x^3}$ | B�� | y=|1-x|��$y=\sqrt{{{��{x-1}��}^2}}$ | ||
| C�� | $y=\frac{{{x^2}-1}}{x-1}$��y=x+1 | D�� | y=x0��y=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{26}{15}$ | B�� | $\frac{13}{15}$ | C�� | -$\frac{26}{15}$ | D�� | -$\frac{13}{15}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com