
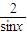 (x∈(0,π))的最小值是2
(x∈(0,π))的最小值是2 ;②在△ABC中,若sin2A=sin2B,则△ABC是等腰或直角三角形;③如果正实数a,b,c满足a + b>c则
;②在△ABC中,若sin2A=sin2B,则△ABC是等腰或直角三角形;③如果正实数a,b,c满足a + b>c则 +
+ >
> ;④如果y=f(x)是可导函数,则f′(x)=0是函数y=f(x)在x=x处取到极值的必要不充分条件.其中正确的命题是( )
;④如果y=f(x)是可导函数,则f′(x)=0是函数y=f(x)在x=x处取到极值的必要不充分条件.其中正确的命题是( ) 或A=B,则三角形形状可判断出.构造函数y=
或A=B,则三角形形状可判断出.构造函数y= ,根据函数的单调性可证得结论;由函数极值点与导数的关系,我们易判断对错.
,根据函数的单调性可证得结论;由函数极值点与导数的关系,我们易判断对错. ≥2
≥2 ,当sinx=
,当sinx= 时取等号,而sinx的最大值是1,故不正确;
时取等号,而sinx的最大值是1,故不正确; 或A=B
或A=B ,该函数在(0.+∞)上单调递增,a+b>c则
,该函数在(0.+∞)上单调递增,a+b>c则 +
+ >
>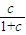 ,故正确;
,故正确;

科目:高中数学 来源: 题型:
| 2 |
| sinx |
| 2 |
| a |
| 1+a |
| b |
| 1+b |
| c |
| 1+c |
| A、①②③ | B、① | C、②③ | D、③ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| sinx |
| 2 |
| a |
| 1+a |
| b |
| 1+b |
| c |
| 1+c |
| A、①②③④ | B、①④ |
| C、②③④ | D、②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| x |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| x |
| 1 |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2013届江西省高二下学期期中考试文科数学试卷(解析版) 题型:填空题
下列命题中:①函数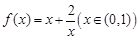 的最小值是
的最小值是 ;②对于任意实数
;②对于任意实数 ,有
,有 且
且 时,
时, ,
,
 ,则
,则 时,
时, ;③如果
;③如果 是可导函数,则
是可导函数,则 是函数
是函数 在
在 处取到极值的必要不充分条件;④已知存在实数
处取到极值的必要不充分条件;④已知存在实数 使得不等式
使得不等式 成立,则实数
成立,则实数 的取值范围是
的取值范围是 。其中正确的命题是___________.
。其中正确的命题是___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com