
分析 (1)先求得P(x),再由f(x)=Q(x)-P(x),由分段函数式可得所求;
(2)分别求出各段的最值,注意运用一次函数和二次函数的最值求法,即可得到.
解答 解:(1)由题意得P(x)=12+10x,…(1分)
则f(x)=Q(x)-P(x)=$\left\{\begin{array}{l}{-0.5{x}^{2}+22x-12-10x,0≤x≤16}\\{224-12-10x,x>16}\end{array}\right.$
即为f(x)=$\left\{\begin{array}{l}{-0.5{x}^{2}+12x-12,0≤x≤16}\\{212-10x,x>16}\end{array}\right.$…(4分)
(2)当x>16时,函数f(x)递减,即有f(x)<f(16)=212-160=52万元 …6 分
当0≤x≤16时,函数f(x)=-0.5x2+12x-12
=-0.5(x-12)2+60,
当x=12时,f(x)有最大值60万元.…9 分
所以当工厂生产12百台时,可使利润最大为60万元.…10 分
点评 本题考查函数模型在实际问题中的应用,考查函数的最值问题,正确求出分段函数式,求出各段的最值是解题的关键,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
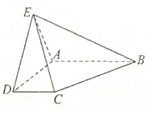 如图,四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,且AB=2CD,侧面ADE为等边三角形,侧面ABE为等腰直角三角形,且角A为直角,且平面ABE⊥平面ADE.
如图,四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,且AB=2CD,侧面ADE为等边三角形,侧面ABE为等腰直角三角形,且角A为直角,且平面ABE⊥平面ADE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {2,4} | C. | {4,6} | D. | {2,4,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
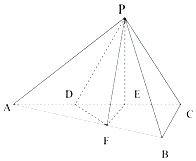 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,点D,E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥平面PBC.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,点D,E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥平面PBC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com