Question

【题目】已知.

（1）若x，，求，的值；

（2）若x，，试判断的奇偶性；

（3）若函数在其定义域上是增函数，，，求实数的取值范围.

Answer 1

【答案】（1）f（1）＝0，f（1）＝0（2）见解析（3）{x|2＜x≤4}

【解析】

（1）利用已知条件，通过赋值法即可f（1），f（﹣1）的值；

（2）通过（1）f（﹣1）＝0，利用函数的奇偶性定义，判断y＝f（x）的奇偶性；

（3）利用函数f（x）在其定义域（0，+∞）上是增函数，结合f（2）＝1，f（x）+f（x﹣2）≤3，得到不等式组，即可求x的取值范围．

解；（1）令x＝y＝1，则f（1）＝f（1）+f（1），所以f（1）＝0；

又令x＝y＝﹣1，则f（1）＝f（﹣1）+f（﹣1），所以f（﹣1）＝0；

（2）令y＝﹣1，则f（﹣x）＝f（x）+f（﹣1），由（1）知f（﹣1）＝0

所以f（﹣x）＝f（x），即函数f（x）为偶函数，

（3）因为f（4）＝f（2）+f（2）＝1+1＝2

所以f（8）＝f（2）+f（4）＝1+2＝3

因为f（x）+f（x﹣2）≤3

所以f[x（x﹣2）]≤f（8）

因为f（x）在（0，+∞）上是增函数

所以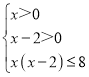，即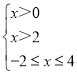

所以{x|2＜x≤4}，所以不等式的解集为{x|2＜x≤4}