


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:山东省泰安市2006—2007学年度第一学期高三期中考试、数学试题(理科) 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省高三下学期期中考试理数 题型:解答题
【必做题】第22题和第23题为必做题, 每小题10分,共20分.要写出必要的文字说明或演算步骤.
有甲、乙两个箱子,甲箱中有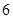 张卡片,其中
张卡片,其中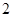 张写有数字
张写有数字 ,
,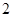 张写有数字
张写有数字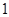 ,
,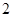 张写有数字
张写有数字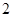 ;乙箱中也有
;乙箱中也有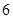 张卡片,其中
张卡片,其中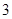 张写有数字
张写有数字 ,
,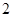 张写有数字
张写有数字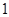 ,
,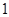 张写有数字
张写有数字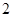 .
.
(1)如果从甲、乙箱中各取一张卡片,设取出的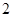 张卡片上数字之积为
张卡片上数字之积为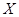 ,求
,求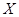 的
的
分布列及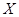 的数学期望;
的数学期望;
(2)如果从甲箱中取一张卡片,从乙箱中取两张卡片,那么取出的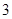 张卡片都写有
张卡片都写有
数字 的概率是多少?
的概率是多少?
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com