
【题目】已知函数 ![]() .
.
(1)求该函数的最小正周期;
(2)求该函数的单调递减区间;
(3)用“五点法”作出该函数在长度为一个周期的闭区间上的简图.
科目:高中数学 来源: 题型:
【题目】某县一中计划把一块边长为20米的等边三角形ABC的边角地辟为植物新品种实验基地,图中DE需把基地分成面积相等的两部分,D在AB上,E在AC上. 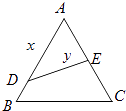
(1)设AD=x(x≥10),ED=y,试用x表示y的函数关系式;
(2)如果DE是灌溉输水管道的位置,为了节约,则希望它最短,DE的位置应该在哪里?如果DE是参观线路,则希望它最长,DE的位置又应该在哪里?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+1,x∈N* , 若x0 , n∈N* , 使f(x0)+f(x0+1)+…+f(x0+n)=63成立,则称(x0 , n)为函数f(x)的一个“生成点”,函数f(x)的“生成点”共有( )
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)上的点A(4,t)到其焦点F的距离为5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)过点F作直线l,使得抛物线C上恰有三个点到直线1的距离为2,求直线1的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙、丙、丁四位同学中选拔一位成绩较稳定的优秀选手,参加山东省职业院校技能大赛,在同样条件下经过多轮测试,成绩分析如表所示,根据表中数据判断,最佳人选为( ) 成绩分析表
甲 | 乙 | 丙 | 丁 | |
平均成绩 | 96 | 96 | 85 | 85 |
标准差s | 4 | 2 | 4 | 2 |
A.甲
B.乙
C.丙
D.丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1、F2为双曲线的焦点,过F2垂直于实轴的直线交双曲线于A、B两点,BF1交y轴于点C,若AC⊥BF1 , 则双曲线的离心率为( )
A.![]()
B.![]()
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A(x1 , y1),B(x2 , y2)是椭圆 ![]() 上的两点,已知向量
上的两点,已知向量 ![]() =(
=( ![]() ,
, ![]() ),
), ![]() =(
=( ![]() ,
, ![]() ),若
),若 ![]() =0且椭圆的离心率e=
=0且椭圆的离心率e= ![]() ,短轴长为2,O为坐标原点.
,短轴长为2,O为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,△ABC的面积为S,(a2+b2)tanC=8S,且sinAcosB=2cosAsinB,则cosA= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com