
【题目】已知函数f(x)= ![]() sin2x+2cos2x+m(0≤x≤
sin2x+2cos2x+m(0≤x≤ ![]() ).
).
(1)若函数f(x)的最大值为6,求常数m的值;
(2)若函数f(x)有两个零点x1和x2 , 求m的取值范围,并求x1和x2的值;
(3)在(1)的条件下,若g(x)=(t﹣1)f(x)﹣ ![]() (t≥2),讨论函数g(x)的零点个数.
(t≥2),讨论函数g(x)的零点个数.
【答案】
(1)解:由题意得,
![]()
= ![]()
∵ ![]() ,∴
,∴ ![]() ,则
,则 ![]() ,
,
∴ ![]() 时,f(x)最大=2×1+1+m=6,
时,f(x)最大=2×1+1+m=6,
解得m=3
(2)解:令 ![]() ,∵
,∵ ![]() ,∴
,∴ ![]() ,
,
函数f(x)在 ![]() 上有两个零点x1,x2方程2sinz=﹣1﹣m在
上有两个零点x1,x2方程2sinz=﹣1﹣m在 ![]() 上有两解.
上有两解.
即函数y=2sinz与y=﹣m﹣1在 ![]() 上有两个交点,
上有两个交点,
由图象可知 ![]() ,解得﹣3<m≤﹣2
,解得﹣3<m≤﹣2
由图象可知 ![]() ,∴
,∴ ![]() ,
,
解得 ![]()
(3)解:在(1)的条件下, ![]() ,
,
且 ![]() ,则
,则 ![]() ,
,
当t≥2时,(t﹣1)f(x)≥3(当t=2且 ![]() 时取等号)
时取等号) ![]()
 ,
,
∵ ![]() ,∴
,∴ ![]() ,
,
![]() (当
(当 ![]() 时取等号)
时取等号)
所以当t=2时,函数 ![]() 有一个零点
有一个零点 ![]()
当t>2时,(t﹣1)f(x)>3 ![]() 恒成立,
恒成立,
函数 ![]() 没有零点
没有零点
【解析】(1)利用二倍角的正弦公式,两角和的正弦公式化简解析式,由x的范围求出 ![]() 的范围,由正弦函数的最大值和条件列出方程,求出m的值;(2)由x的范围求出z=
的范围,由正弦函数的最大值和条件列出方程,求出m的值;(2)由x的范围求出z= ![]() 的范围,将函数f(x)有两个零点转化为:方程2sinz=﹣1﹣m在
的范围,将函数f(x)有两个零点转化为:方程2sinz=﹣1﹣m在 ![]() 上有两解,再转化为两个函数图象有两个交点,由正弦函数的图象列出不等式,求出m的范围,由正弦函数的图象和对称性求出x1与x2的和;(3)由(1)求出f(x)的最小值,求出当t≥2时(t﹣1)f(x)的范围,利用商的关系、两角差的正切公式化简
上有两解,再转化为两个函数图象有两个交点,由正弦函数的图象列出不等式,求出m的范围,由正弦函数的图象和对称性求出x1与x2的和;(3)由(1)求出f(x)的最小值,求出当t≥2时(t﹣1)f(x)的范围,利用商的关系、两角差的正切公式化简 ![]() ,由x的范围、正切函数的性质求出
,由x的范围、正切函数的性质求出 ![]() 范围,即可判断出函数g(x)的零点个数.
范围,即可判断出函数g(x)的零点个数.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() .
.
(1)若椭圆![]() 的右焦点坐标为
的右焦点坐标为![]() ,求
,求![]() 的值;
的值;
(2)由椭圆![]() 上不同三点构成三角形称为椭圆的内接三角形.若以
上不同三点构成三角形称为椭圆的内接三角形.若以![]() 为直角顶点的椭圆
为直角顶点的椭圆![]() 的内接等腰直角三角形恰有三个,求
的内接等腰直角三角形恰有三个,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
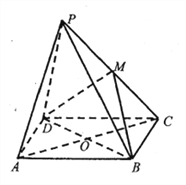
【题目】如图,点![]() 是菱形
是菱形![]() 所在平面外一点,
所在平面外一点, ![]() ,
, ![]() 是等边三角形,
是等边三角形, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 的所成角的大小.
的所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,
中, ![]() 为棱
为棱![]() 上一动点,
上一动点, ![]() 为底面
为底面![]() 上一动点,
上一动点, ![]() 是
是![]() 的中点,若点
的中点,若点![]() 都运动时,点
都运动时,点![]() 构成的点集是一个空间几何体,则这个几何体是
构成的点集是一个空间几何体,则这个几何体是

A. 棱柱 B. 棱台 C. 棱锥 D. 球的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
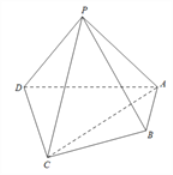
【题目】如图,在四棱锥![]() 中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,
中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2, ![]() .
.
(1)求证:PD⊥平面PAB;
(2)求直线PB与平面PCD所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com