
分析 先选一组基底,再利用向量加法和减法的三角形法则和平行四边形法则将两条异面直线的方向向量用基底表示,最后利用夹角公式求异面直线AB1与BC1所成角的余弦值即可
解答 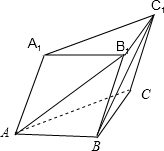 解:如图,设$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,棱长均为1,
解:如图,设$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,棱长均为1,
则$\overrightarrow{a}•\overrightarrow{b}$=$\frac{1}{2}$,$\overrightarrow{b}•\overrightarrow{c}$=$\frac{1}{2}$,$\overrightarrow{a}•\overrightarrow{c}$=$\frac{1}{2}$,
∴$\overrightarrow{A{B}_{1}}$•$\overrightarrow{B{C}_{1}}$=($\overrightarrow{a}$+$\overrightarrow{c}$)•($\overrightarrow{b}$-$\overrightarrow{a}$+$\overrightarrow{c}$)=$\frac{1}{2}-1+\frac{1}{2}+1$=1,
∵|$\overrightarrow{A{B}_{1}}$|=|$\overrightarrow{a}$+$\overrightarrow{c}$|=$\sqrt{3}$,|$\overrightarrow{B{C}_{1}}$|=|$\overrightarrow{b}$-$\overrightarrow{a}$+$\overrightarrow{c}$|=$\sqrt{2}$,
∴cos<$\overrightarrow{A{B}_{1}}$,$\overrightarrow{B{C}_{1}}$>=$\frac{1}{\sqrt{2}×\sqrt{3}}$=$\frac{\sqrt{6}}{6}$,
∴异面直线AB1与BC1所成角的余弦值为 $\frac{\sqrt{6}}{6}$.
点评 本题主要考查了空间向量在解决立体几何问题中的应用,空间向量基本定理,向量数量积运算的性质及夹角公式的应用,有一定的运算量.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=-$\frac{1}{x}$ | B. | f(x)=-$\frac{1}{x-2}$ | C. | f(x)=$\frac{1}{x+2}$ | D. | f(x)=-$\frac{1}{x+2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+(y+2)2=1 | B. | (x-2)2+y2=1 | C. | x2+(y-2)2=1 | D. | (x-2)2+y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com