
【题目】已知数列{an}的前n项和为Sn , 且an是2与Sn的等差中项.
(1)求数列{an}的通项公式;
(2)若 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
【答案】
(1)解:∵an是2与Sn的等差中项,
∴2an=2+Sn,
∴2an﹣1=2+Sn﹣1(n≥2),
两式作差得:2an﹣2an﹣1=an,即 ![]() (n≥2).
(n≥2).
又2a1=2+a1,∴a1=2.
则数列{an}是以2为首项,以2为公比的等比数列,
∴ ![]() ;
;
(2)解: ![]() =
= ![]() .
.
∴ ![]() .
.
![]() .
.
两式作差得: ![]()
= ![]()
= 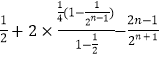
= ![]() .
.
∴ ![]() .
.
【解析】(1)根据题意可得2an=2+Sn,得到2an﹣1=2+Sn﹣1(n≥2),两式作差可得数列{an}是以2为首项,以2为公比的等比数列,代入等比数列的通项公式得到答案。
(2)根据题意可得把数列{an}的通项公式代入b n = ![]() ,再由错位相减法求出数列{bn}的前n项和Tn.
,再由错位相减法求出数列{bn}的前n项和Tn.
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系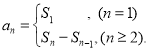 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】为了培养学生的数学建模和应用能力,某校组织了一次实地测量活动,如图,假设待测量的树木 ![]() 的高度
的高度 ![]() ,垂直放置的标杆
,垂直放置的标杆 ![]() 的高度
的高度 ![]() ,仰角
,仰角 ![]() 三点共线),试根据上述测量方案,回答如下问题:
三点共线),试根据上述测量方案,回答如下问题: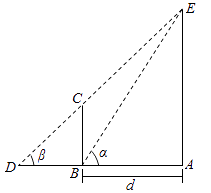
(1)若测得 ![]() ,试求
,试求 ![]() 的值;
的值;
(2)经过分析若干测得的数据后,大家一致认为适当调整标杆到树木的距离 ![]() (单位:)使
(单位:)使 ![]() 与
与 ![]() 之差较大时,可以提高测量的精确度.若树木的实际高为
之差较大时,可以提高测量的精确度.若树木的实际高为 ![]() ,试问
,试问 ![]() 为多少时,
为多少时, ![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin(2x+ ![]() )图象上的每个点的横坐标缩短为原来的一半,纵坐标不变,再将所得图象向左平移
)图象上的每个点的横坐标缩短为原来的一半,纵坐标不变,再将所得图象向左平移 ![]() 个单位得到函数g(x)的图象.在g(x)图象的所有对称中心中,离原点最近的对称中心为( )
个单位得到函数g(x)的图象.在g(x)图象的所有对称中心中,离原点最近的对称中心为( )
A.(﹣ ![]() ,0)
,0)
B.( ![]() ,0)
,0)
C.(﹣ ![]() ,0)
,0)
D.( ![]() ,0)
,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率分布直方图,则下列说法正确的是( )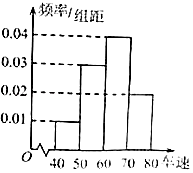
A.平均数为62.5
B.中位数为62.5
C.众数为60和70
D.以上都不对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 的三个内角 A,B,C 成等差数列,且 a,b,c 分别为角 A,B,C 的对边,求证:(a+b)-1+(b+c)-1=3(a+b+c)-1
的三个内角 A,B,C 成等差数列,且 a,b,c 分别为角 A,B,C 的对边,求证:(a+b)-1+(b+c)-1=3(a+b+c)-1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前 n 项和为 Sn ,且(3-m)Sn+2man=m+3(
的前 n 项和为 Sn ,且(3-m)Sn+2man=m+3(![]() ) ,其中 m 为常数,且
) ,其中 m 为常数,且 ![]() .
.
①求证: ![]() 是等比数列;
是等比数列;
②若数列 ![]() 的公比为q=f(m) ,数列 {bn} 满足 b1=a1 ,
的公比为q=f(m) ,数列 {bn} 满足 b1=a1 ,![]() ,求证:
,求证: ![]() 为等差数列.
为等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )
①存在点E使得直线SA⊥平面SBC
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行.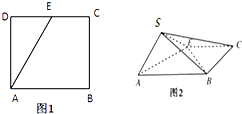
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,满足(2b﹣c)cosA=acosC.
(1)求角A;
(2)若 ![]() ,b+c=5,求△ABC的面积.
,b+c=5,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )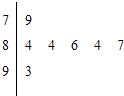
A.84,4.84
B.84,1.6
C.85,1.6
D.85,4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com