练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．如图，E，F分别为正方形的面ADD1A1、BCC1B1的中心，则四边形BFD1E在该正方形上的平行投影不可能为①④．

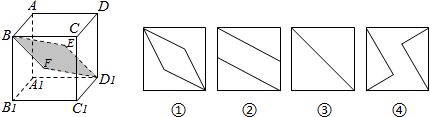
    分析 按照三视图的作法：上下、左右、前后三个方向的射影，四边形的四个顶点在三个投影面上的射影，再将其连接即可得到三个视图的形状，按此规则对题设中所给的四图形进行判断即可．

    解答 解：因为正方体是对称的几何体，
    所以四边形BFD1E在该正方体的面上的射影可分为：自上而下、自左至右、由前及后三个方向的射影，
    也就是在面ABCD、面ABB1A1、面ADD1A1上的射影．
    四边形BFD1E在面ABCD和面ABB1A1上的射影相同，如图②所示；
    四边形BFD1E在该正方体对角面的ABC1D1内，它在面ADD1A1上的射影显然是一条线段，如图③所示．
    故四边形BFD1E在该正方形上的平行投影不可能为①④，
    故答案为：①④．

    点评 本题考查简单空间图形的三视图，考查根据作三视图的规则来作出三个视图的能力，三视图是高考的新增考点，不时出现在高考试题中，应予以重视．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

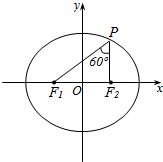    8．如图所示，已知P为椭圆$\frac{{x}^{2}}{25}$+$\frac{4{y}^{2}}{75}$=1上一点，F1，F2是椭圆的焦点，∠F1PF2=60°，求△F1PF2的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．某工厂生产某种产品，成本C（单位：万元）与年产量x，（0≤x≤15，单位：千台）的函数关系为C（x）=2-x．销售收入S：（单位：万元）与年产量x有函数关系S（x）=$-{\frac{1}{3}x}^{2}$+5x．
    （1）试求利润y与产量x的关系式；
    （2）年产量为多少台时利润最大，最大利润是多少？（总利润=总收益-总成本）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．数列{an}的前n项和为Sn，且满足S1=2，Sn+1=3Sn+2．
    （1）证明：{Sn+1}是等比数列，并求数列{an}的通项公式an；
    （2）设b1=$\frac{1}{2}$，bn=$\frac{{a}_{n}}{{S}_{n-1}•{S}_{n}}$（n≥2），求证：b1+b2+…+bn＜1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知a＞0，b＞0，且2a+b=2，则ab的最大值为$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．设θ是第三象限角，且满足|sin$\frac{θ}{2}$|=-sin$\frac{θ}{2}$，试判断$\frac{θ}{2}$所在象限．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．若函数y=f（x）=$\frac{a•{2}^{x}-1-a}{{2}^{x}-1}$为奇函数．
    （1）确定a的值；
    （2）求函数的定义域；
    （3）求函数的值域；
    （4）讨论函数的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

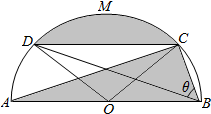    7．如图：阴影部分是一个机械构件．该构件是由一块半圆形铁皮剪切后，剩下了弓形面CMD，及三角形ABC所形成的．其中半圆直径AB=8，CD∥AB，点M是$\widehat{CD}$上一点，∠CBD=θ．
    （1）求弓形面CMD的面积与θ的函数解析式k（θ）；
    （2）求这个构件的面积关于θ的函数解析式S（θ）；并求S（θ）的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=lnx．
    （1）求函数f（x）的图象在x=1处的切线方程；
    （2）若函数y=f（x）+$\frac{k}{x}$在[$\frac{1}{{e}^{2}}$，+∞）上有两个不同的零点，求实数k的取值范围；
    （3）是否存在实数k，使得对任意的x∈（$\frac{1}{2}$，+∞），都有函数y=f（x）+$\frac{k}{x}$的图象在g（x）=$\frac{{e}^{x}}{x}$的图象的下方；若存在，请求出最大整数k的值，若不存在，请说明理由（参考数据：ln2=0.6931，e${\;}^{\frac{1}{2}}$=1.6487）．

    查看答案和解析>>

    同步练习册答案