
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,原点到椭圆的上顶点与右顶点连线的距离为
,原点到椭圆的上顶点与右顶点连线的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)斜率存在且不为零的直线![]() 与椭圆相交于
与椭圆相交于![]() ,
,![]() 两点,若线段
两点,若线段![]() 的垂直平分线的纵截距为-1,求直线
的垂直平分线的纵截距为-1,求直线![]() 纵截距的取值范围.
纵截距的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由离心率为![]() ,可以得到
,可以得到![]() 的关系,由原点到椭圆的上顶点与右顶点连线的距离为
的关系,由原点到椭圆的上顶点与右顶点连线的距离为![]() ,可以得到
,可以得到![]() 的关系,结合
的关系,结合![]() ,求出
,求出![]() ,写出椭圆标准方程;
,写出椭圆标准方程;
(2)设出斜率存在且不为零的直线![]() 的直线方程,与椭圆方程联立,得到一个关于
的直线方程,与椭圆方程联立,得到一个关于![]() 的一元二次方程,由根的判断式大于零,得到一个不等式
的一元二次方程,由根的判断式大于零,得到一个不等式![]() ,设
,设![]() 中点
中点![]() ,利用根与系数关系可以求出坐标,结合已知,通过斜率公式,可以得到
,利用根与系数关系可以求出坐标,结合已知,通过斜率公式,可以得到![]() ,结合求出的不等式,可以求出直线
,结合求出的不等式,可以求出直线![]() 纵截距的取值范围.
纵截距的取值范围.
解:(1)原点到椭圆上顶点与右顶点连线的距离为![]() .
.
又离心率![]() ,又因为
,又因为![]() ,
,
解得![]() ,
,![]() ,所以椭圆
,所以椭圆![]() 方程为
方程为![]() .
.
(2)设![]() ,直线
,直线![]() 的方程为:
的方程为:![]() ,
,
将![]() 代入
代入![]() 得:
得:
![]() ,
,
于是![]() 得:
得:![]()
且![]() ,
,
设![]() 中点
中点![]() ,则
,则![]() ,
,![]()
因为线段![]() 的垂直平分线的纵截距为
的垂直平分线的纵截距为![]() ,所以线段
,所以线段![]() 的垂直平分线过点
的垂直平分线过点![]() ,
,
所以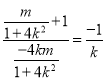 ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() , 所以
, 所以![]() ,
,
![]() 代入
代入![]() 得
得![]() ,
,
所以![]() .
.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就,在“杨辉三角”中,第![]() 行的所有数字之和为
行的所有数字之和为![]() ,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前15项和为( )
,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前15项和为( )
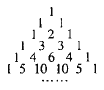
A. 110B. 114C. 124D. 125
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图是2017年第一季度五省GDP情况图,则下列陈述中不正确的是( )
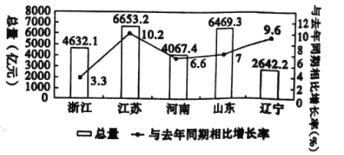
A. 2017年第一季度GDP增速由高到低排位第5的是浙江省.
B. 与去年同期相比,2017年第一季度的GDP总量实现了增长.
C. 去年同期河南省的GDP总量不超过4000亿元 .
D. 2017年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生社团组织活动丰富,学生会为了解同学对社团活动的满意程度,随机选取了100位同学进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[40,50),[50,60),[60,70),…,[90,100]分成6组,制成如图所示频率分布直方图.
(1)求图中x的值;
(2)求这组数据的中位数;
(3)现从被调查的问卷满意度评分值在[60,80)的学生中按分层抽样的方法抽取5人进行座谈了解,再从这5人中随机抽取2人作主题发言,求抽取的2人恰在同一组的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱锥![]() 中,O为顶点S在底面ABCD内的投影,P为侧棱SD的中点,且
中,O为顶点S在底面ABCD内的投影,P为侧棱SD的中点,且![]() .
.
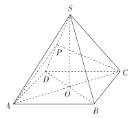
(1)证明:![]() 平面PAC.
平面PAC.
(2)求直线BC与平面PAC的所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面四边形![]() 中,
中,![]() ,
,![]() 是
是![]() ,
,![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起至
折起至![]() ,使平面
,使平面![]() ,则四面体
,则四面体![]() 中,下列结论不正确的是( )
中,下列结论不正确的是( )
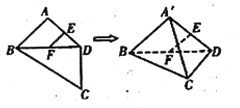
A.![]() 平面
平面![]()
B.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
C.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
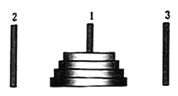
【题目】如图所示,有三根针和套在一根针上的![]() 个金属片,按下列规则,把金属片从一根针上全部移到另一根针上.
个金属片,按下列规则,把金属片从一根针上全部移到另一根针上.
(1)每次只能移动一个金属片;
(2)在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面.
将![]() 个金属片从1号针移到3号针最少需要移动的次数记为
个金属片从1号针移到3号针最少需要移动的次数记为![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间四边形ABCD中,H,G分别是AD,CD的中点,E,F分别边AB,BC上的点,且![]() ;
;

求证:(1)点E,F,G,H四点共面;
(2)直线EH,BD,FG相交于同一点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )为奇函数,且相邻两对称轴间的距离为
)为奇函数,且相邻两对称轴间的距离为![]() .
.
(1)当![]() 时,求
时,求![]() 的单调递减区间;
的单调递减区间;
(2)将函数![]() 的图象沿
的图象沿![]() 轴方向向右平移
轴方向向右平移![]() 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象.当时
的图象.当时![]() ,求函数
,求函数![]() 的值域.
的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com