
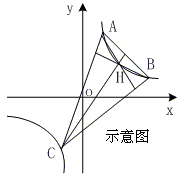
(1)在双曲线xy=1上任取不同三点A、B、C,证明△ABC的垂心H也在该双曲线上.
(2)若A、B是双曲线xy=1在第一象限内的一支上的两点,且|AB|=2.求线段AB的中点M的轨迹方程;
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源:江苏省常州二中2008高考一轮复习综合测试3、数学(文科) 题型:044
(1)在双曲线xy=1上任取不同三点A、B、C,证明:⊿ABC的垂心H也在该双曲线上;
(2)若正三角形ABC的一个顶点为C(―1,―1),另两个顶点A、B在双曲线xy=1另一支上,求顶点A、B的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com