
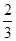 (2)
(2)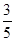 (3)
(3)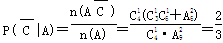 . 4分
. 4分 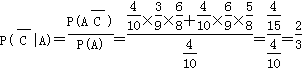 . 4分
. 4分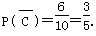 6分
6分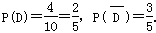
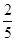 ).
).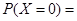
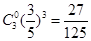 ,
,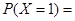
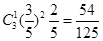 ,
,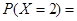
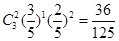 ,
,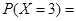
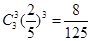 10分
10分| X | 0 | 1 | 2 | 3 |
| P | 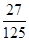 | 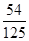 |  |  |
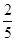 ). 12分
). 12分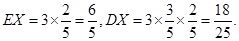 14分
14分

科目:高中数学 来源:不详 题型:单选题
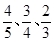 ,在实际操作考试中“合格”的概率依次为
,在实际操作考试中“合格”的概率依次为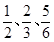 ,所有考试是否合格相互之间没有影响。
,所有考试是否合格相互之间没有影响。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
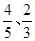 ,在操作考试中“合格”的概率依次为
,在操作考试中“合格”的概率依次为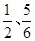 ,所有考试是否合格,相互之间没有影响.则甲、乙进行理论与操作两项考试后,恰有1人获得“合格证书”的概率 .
,所有考试是否合格,相互之间没有影响.则甲、乙进行理论与操作两项考试后,恰有1人获得“合格证书”的概率 .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
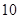 道题中,甲答对其中每道题的概率都是
道题中,甲答对其中每道题的概率都是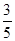 ,乙能答对其中的
,乙能答对其中的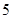 道题.规定每次考试都从备选的
道题.规定每次考试都从备选的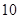 道题中随机抽出
道题中随机抽出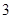 道题进行测试,答对一题加
道题进行测试,答对一题加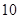 分,答错一题(不答视为答错)减
分,答错一题(不答视为答错)减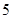 分,至少得
分,至少得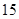 分才能入选.
分才能入选.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
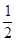 和
和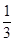 , 甲、乙两人各射击一次,有下列说法: ① 目标恰好被命中一次的概率为
, 甲、乙两人各射击一次,有下列说法: ① 目标恰好被命中一次的概率为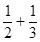 ;② 目标恰好被命中两次的概率为
;② 目标恰好被命中两次的概率为 ; ③ 目标被命中的概率为
; ③ 目标被命中的概率为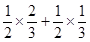 ; ④ 目标被命中的概率为
; ④ 目标被命中的概率为 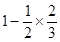 。以上说法正确的序号依次是
。以上说法正确的序号依次是 | A.②③ | B.①②③ | C.②④ | D.①③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,乙解出它的概率为
,乙解出它的概率为 ,丙解出它的概率为
,丙解出它的概率为 ,则
,则
|
 B.
B. C.
C.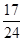 D.1
D.1查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
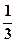 ,
,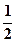 ,
,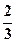 ,则汽车在这三处因遇红灯而停车一次的概率为( )
,则汽车在这三处因遇红灯而停车一次的概率为( )A.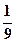 | B.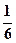 | C.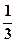 | D.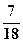 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com