
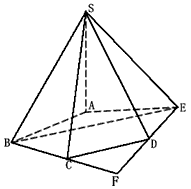
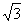 ,∠BAE=∠BCD=∠CDE=120°,
,∠BAE=∠BCD=∠CDE=120°,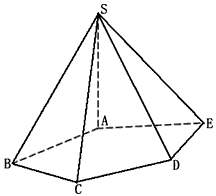
| 解:(Ⅰ)连结BE,延长BC、ED交于点F, 则∠DCF=∠CDF=60°, ∴△CDF为正三角形, ∴CF=DF, 又BC=DE, ∴BF=EF, 因此,△BFE为正三角形, ∴∠FBE=∠FCD=60°, ∴BE∥CD, 所以∠SBE(或其补角)就是异面直线CD与SB所成的角, ∵SA⊥底面ABCDE,且SA=AB=AE=2, ∴SB=  , ,又∠BAE=120°, 所以BE= 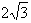 , ,从而 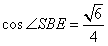 , ,∴∠SBE= 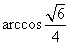 , ,所以异面直线CD与SB所成的角为  。 。(Ⅱ)由题意,△ABE是等腰三角形,∠BAE=120°, 所以∠ABE=30°, 又∠FBE=60°, ∴∠ABC=90°, 所以BC⊥BA, ∵SA⊥底面ABCDE,BC  底面ABCDE, 底面ABCDE, ∴SA⊥BC, 又SA∩BA=A, ∴BC⊥平面SAB。 (Ⅲ)二面角B-SC-D的大小为 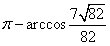 。 。 |
 |


科目:高中数学 来源:不详 题型:单选题
A.-
| B.
| C.
| D.-
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
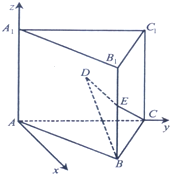
查看答案和解析>>
科目:高中数学 来源:湖北模拟 题型:单选题
A.
| B.
| C.
| D.
|
查看答案和解析>>
科目:高中数学 来源:0115 同步题 题型:单选题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com