
【题目】2018年2月22日,在韩国平昌冬奥会短道速滑男子500米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造中国男子冰上竞速项目在冬奥会金牌零的突破.某高校为调查该校学生在冬奥会期间累计观看冬奥会的时间情况,收集了200位男生、100位女生累计观看冬奥会时间的样本数据(单位:小时).又在100位女生中随机抽取20个人,已知这20位女生的数据茎叶图如图所示.
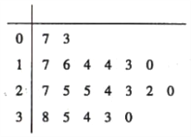

(I)将这20位女生的时间数据分成8组,分组区间分别为![]()
![]() ,
,![]() ,…,
,…,![]() ,
,![]()
![]() ,完成频率分布直方图;
,完成频率分布直方图;
(II)以(I)中的频率作为概率,求1名女生观看冬奥会时间不少于30小时的概率;(III)以(I)中的频率估计100位女生中累计观看时间小于20个小时的人数,已知200位男生中累计观看时间小于20小时的男生有50人.请完成下面的列联表,并判断是否有99%的把握认为“该校学生观看冬奥会累计时间与性别有关”.
男生 | 女生 |
| |
累计观看时间小于20小时 | |||
累计观看时间小于20小时 | |||
总计 | 300 |
附:(![]()
![]() ).
).
【答案】(1)见解析.
(2)![]() .
.
(3)列联表见解析;有99%的把握认为“该校学生观看冬奥会累计时间与性别有关”.
【解析】分析:(1)根据提干茎叶图数据计算得到相应的频率,从而得到频率分布直方图;(2). 因为(1)中![]() 的频率为
的频率为![]() ,以频率估计概率;(3)补充列联表,计算得到卡方值即可做出判断.
,以频率估计概率;(3)补充列联表,计算得到卡方值即可做出判断.
详解:
(1)由题意知样本容量为20,频率分布直方图为:
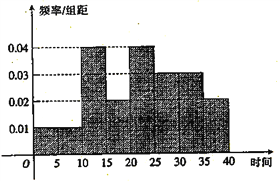
(2)因为(1)中![]() 的频率为
的频率为![]() ,
,
所以1名女生观看冬奥会时间不少于30小时的概率为![]() .
.
(3)因为(1)中![]() 的频率为,故可估计100位女生中累计观看时间小于20小时的人数是
的频率为,故可估计100位女生中累计观看时间小于20小时的人数是![]()
![]() .
.
所以累计观看时间与性别列联表如下:
男生 | 女生 | 总计 | |
累计观看时间小于20小时 | 50 | 40 | 90 |
累计观看时间小于20小时 | 150 | 60 | 210 |
总计 | 200 | 100 | 300 |
结合列联表可算得![]()
所以,有99%的把握认为“该校学生观看冬奥会累计时间与性别有关”.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为 ![]() .(12分)
.(12分)
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任从本班![]() 名男生,
名男生,![]() 名女生中随机抽取一个容量为
名女生中随机抽取一个容量为![]() 的样本,对他们的数学及物理成绩进行分析,这
的样本,对他们的数学及物理成绩进行分析,这![]() 名同学的数学及物理成绩(单位:分数)对应如下表:
名同学的数学及物理成绩(单位:分数)对应如下表:
学生序号 |
|
|
|
|
|
|
|
数学成绩 |
|
|
|
|
|
|
|
物理成绩 |
|
|
|
|
|
|
|
(1)根据以上数据,求物理成绩![]() 关于数学成绩
关于数学成绩![]() 的线性回归方程(系数均精确到
的线性回归方程(系数均精确到![]() ),并预测班上某位数学成绩为
),并预测班上某位数学成绩为![]() 分的同学的物理成绩(保留到整数);
分的同学的物理成绩(保留到整数);
(2)从物理成绩不低于![]() 分的样本学生中随机抽取
分的样本学生中随机抽取![]() 人,求抽到的
人,求抽到的![]() 人数学成绩也不低于
人数学成绩也不低于![]() 分的概率.
分的概率.
参考公式:
已经计算出:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则 ![]() 的取值范围是( )
的取值范围是( ) 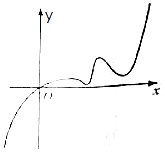
A.( ![]() ,2)
,2)
B.(﹣∞, ![]() )∪(2,+∞)
)∪(2,+∞)
C.(2,+∞)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则 ![]() 的取值范围是( )
的取值范围是( ) 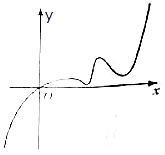
A.( ![]() ,2)
,2)
B.(﹣∞, ![]() )∪(2,+∞)
)∪(2,+∞)
C.(2,+∞)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,函数
,函数![]() ,
,![]() 是函数
是函数![]() 的导函数,
的导函数, ![]() 是自然对数的底数.
是自然对数的底数.
(1)当![]() 时,求导函数
时,求导函数![]() 的最小值;
的最小值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(3)若函数![]() 存在极大值与极小值,求实数
存在极大值与极小值,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象如图所示(其中
的图象如图所示(其中![]() 是定义域为
是定义域为![]() 的函数
的函数![]() 的导函数),则以下说法错误的是( ).
的导函数),则以下说法错误的是( ).
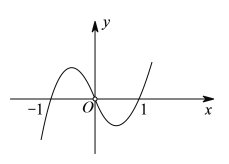
A. ![]()
B. 当![]() 时,函数
时,函数![]() 取得极大值
取得极大值
C. 方程![]() 与
与![]() 均有三个实数根
均有三个实数根
D. 当![]() 时,函数
时,函数![]() 取得极小值
取得极小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)上的点到右焦点F的最小距离是
=1(a>b>0)上的点到右焦点F的最小距离是 ![]() ﹣1,F到上顶点的距离为
﹣1,F到上顶点的距离为 ![]() ,点C(m,0)是线段OF上的一个动点.
,点C(m,0)是线段OF上的一个动点.
(1)求椭圆的方程;
(2)是否存在过点F且与x轴不垂直的直线l与椭圆交于A、B两点,使得( ![]() +
+ ![]() )⊥
)⊥ ![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市食品药品监督管理局开展2019年春季校园餐饮安全检查,对本市的8所中学食堂进行了原料采购加工标准和卫生标准的检查和评分,其评分情况如下表所示:
中学编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
原料采购加工标准评分x | 100 | 95 | 93 | 83 | 82 | 75 | 70 | 66 |
卫生标准评分y | 87 | 84 | 83 | 82 | 81 | 79 | 77 | 75 |
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;(精确到0.1)
(2)现从8个被检查的中学食堂中任意抽取两个组成一组,若两个中学食堂的原料采购加工标准和卫生标准的评分均超过80分,则组成“对比标兵食堂”,求该组被评为“对比标兵食堂”的概率.
参考公式: ,
,![]() ;
;
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com