
【题目】已知函数f(x)=(1+x)e﹣2x , g(x)=ax+ ![]() +1+2xcosx,当x∈[0,1]时,
+1+2xcosx,当x∈[0,1]时,
(1)求证: ![]() ;
;
(2)若f(x)≥g(x)恒成立,求实数a的取值范围.
【答案】
(1)证明:①当x∈[0,1)时,(1+x)e﹣2x≥1﹣x(1+x)e﹣x≥(1﹣x)ex,
令h(x)=(1+x)e﹣x﹣(1﹣x)ex,则h′(x)=x(ex﹣e﹣x).
当x∈[0,1)时,h′(x)≥0,
∴h(x)在[0,1)上是增函数,
∴h(x)≥h(0)=0,即f(x)≥1﹣x.
②当x∈[0,1)时, ![]() ex≥1+x,令u(x)=ex﹣1﹣x,则u′(x)=ex﹣1.
ex≥1+x,令u(x)=ex﹣1﹣x,则u′(x)=ex﹣1.
当x∈[0,1)时,u′(x)≥0,
∴u(x)在[0,1)单调递增,∴u(x)≥u(0)=0,
∴f(x) ![]() .
.
综上可知: ![]() .
.
(2)解:设G(x)=f(x)﹣g(x)= ![]()
≥ ![]() =
= ![]() .
.
令H(x)= ![]() ,则H′(x)=x﹣2sinx,
,则H′(x)=x﹣2sinx,
令K(x)=x﹣2sinx,则K′(x)=1﹣2cosx.
当x∈[0,1)时,K′(x)<0,
可得H′(x)是[0,1)上的减函数,∴H′(x)≤H′(0)=0,故H(x)在[0,1)单调递减,
∴H(x)≤H(0)=2.∴a+1+H(x)≤a+3.
∴当a≤﹣3时,f(x)≥g(x)在[0,1)上恒成立.
下面证明当a>﹣3时,f(x)≥g(x)在[0,1)上不恒成立.
f(x)﹣g(x)≤ ![]() =
= ![]() =﹣x
=﹣x ![]() .
.
令v(x)= ![]() =
= ![]() ,则v′(x)=
,则v′(x)= ![]() .
.
当x∈[0,1)时,v′(x)≤0,故v(x)在[0,1)上是减函数,
∴v(x)∈(a+1+2cos1,a+3].
当a>﹣3时,a+3>0.
∴存在x0∈(0,1),使得v(x0)>0,此时,f(x0)<g(x0).
即f(x)≥g(x)在[0,1)不恒成立.
综上实数a的取值范围是(﹣∞,﹣3].
【解析】(1)①当x∈[0,1)时,(1+x)e﹣2x≥1﹣x(1+x)e﹣x≥(1﹣x)ex , 令h(x)=(1+x)e﹣x﹣(1﹣x)ex , 利用导数得到h(x)的单调性即可证明;②当x∈[0,1)时, ![]() ex≥1+x,令u(x)=ex﹣1﹣x,利用导数得出h(x)的单调性即可证明.(2)利用(I)的结论得到f(x)≥1﹣x,于是G(x)=f(x)﹣g(x)≥
ex≥1+x,令u(x)=ex﹣1﹣x,利用导数得出h(x)的单调性即可证明.(2)利用(I)的结论得到f(x)≥1﹣x,于是G(x)=f(x)﹣g(x)≥ ![]() =
= ![]() .再令H(x)=
.再令H(x)= ![]() ,通过多次求导得出其单调性即可求出a的取值范围.
,通过多次求导得出其单调性即可求出a的取值范围.
【考点精析】利用利用导数研究函数的单调性和函数的极值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=alnx-bx2(x>0),若函数f(x)在x=1处与直线y=-![]() 相切。
相切。
(1)求实数a,b的值;
(2)求函数f(x)在![]() 上的最大值。
上的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() 的外接圆圆心为
的外接圆圆心为![]() .
.
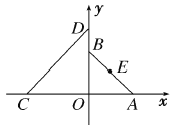
(1)若![]() 与直线
与直线![]() 相切,求实数
相切,求实数![]() 的值;
的值;
(2)设点![]() 在
在![]() 上,使
上,使![]() 的面积等于12的点
的面积等于12的点![]() 有且只有三个,试问这样的
有且只有三个,试问这样的![]() 是否存在?若存在求出
是否存在?若存在求出![]() 的标准方程;若不存在,说明理由.
的标准方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数有( )
①用 刻画回归效果,当
刻画回归效果,当![]() 越大时,模型的拟合效果越差;反之,则越好;
越大时,模型的拟合效果越差;反之,则越好;
②命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;
”;
③若回归直线的斜率估计值是![]() ,样本点的中心为
,样本点的中心为![]() ,则回归直线方程是
,则回归直线方程是![]() ;
;
④综合法证明数学问题是“由因索果”,分析法证明数学问题是“执果索因”。
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)已知过原点的动直线![]() 与圆
与圆![]()
![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(1)求圆![]() 的圆心坐标;
的圆心坐标;
(2)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得直线
,使得直线![]()
![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n=( ) 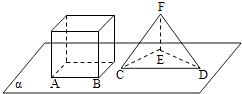
A.8
B.9
C.10
D.11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小波以游戏方式决定是参加学校合唱团还是参加学校排球队,游戏规则为:以0为起点,再从A1 , A2 , A3 , A4 , A5 , A6 , A7 , A8(如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X.若X=0就参加学校合唱团,否则就参加学校排球队. 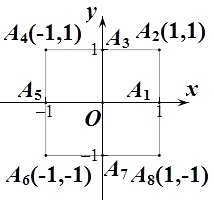
(1)求小波参加学校合唱团的概率;
(2)求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直棱柱ABC﹣A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB= ![]() AB.
AB. 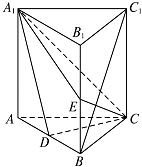
(1)证明:BC1∥平面A1CD
(2)求二面角D﹣A1C﹣E的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com