
【题目】如图,已知四棱锥![]() 的底面
的底面![]() 为棱形,且
为棱形,且![]() 面
面![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
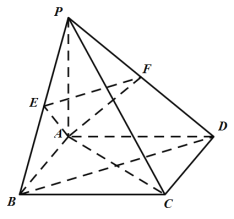
(1)求证:![]() 面
面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】如图是甲、乙、丙三个企业的产品成本(单位:万元)及其构成比例,则下列判断正确的是( )

A. 乙企业支付的工资所占成本的比重在三个企业中最大
B. 由于丙企业生产规模大,所以它的其他费用开支所占成本的比重也最大
C. 甲企业本着勤俭创业的原则,将其他费用支出降到了最低点
D. 乙企业用于工资和其他费用支出额比甲丙都高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两种理财产品![]() 和
和![]() ,投资这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
,投资这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品![]() :
:
投资结果 | 获利 | 不赔不赚 | 亏损 |
概率 |
|
|
|
产品![]() :
:
投资结果 | 获利 | 不赔不赚 | 亏损 |
概率 |
|
|
|
注:![]()
(1)若甲、乙两人分别选择了产品![]() 投资,一年后他们中至少有一人获利的概率大于
投资,一年后他们中至少有一人获利的概率大于![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)若丙要将20万元人民币投资其中一种产品,以一年后的投资收益的期望值为决策依据,则丙选择哪种产品投资较为理想.
查看答案和解析>>
科目:高中数学 来源: 题型:
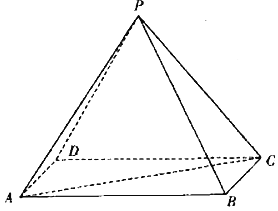
【题目】如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,AB=2AD=2,∠DAB=60°,PA=PC=2,且平面ACP⊥平面ABCD.
(Ⅰ)求证:CB⊥PD;
(Ⅱ)求二面角C-PB-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科研人员在对人体脂肪含量和年龄之间关系的研究中,获得了一些年龄和脂肪含量的简单随机样本数据,如下表:

根据上表的数据得到如下的散点图.
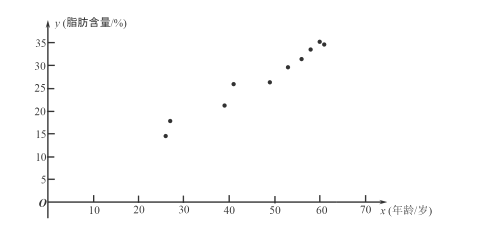
(1)根据上表中的样本数据及其散点图:
(i)求![]() ;
;
(ii)计算样本相关系数(精确到0.01),并刻画它们的相关程度.
(2)若y关于x的线性回归方程为![]() ,求
,求![]() 的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量。
的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量。
附:参考数据: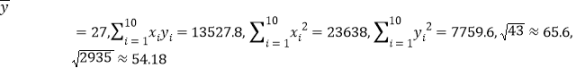
参考公式:相关系数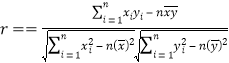
回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为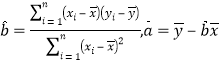
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年东京夏季奥运会将设置![]() 米男女混合泳接力这一新的比赛项目,比赛的规则是:每个参赛国家派出2男2女共计4名运动员参加比赛,按照仰泳
米男女混合泳接力这一新的比赛项目,比赛的规则是:每个参赛国家派出2男2女共计4名运动员参加比赛,按照仰泳![]() 蛙泳
蛙泳![]() 蝶泳
蝶泳![]() 自由泳的接力顺序,每种泳姿100米且由1名运动员完成,且每名运动员都要出场,若中国队确定了备战该项目的4名运动员名单,其中女运动员甲只能承担仰泳或者自由泳,男运动员乙只能承担蝶泳或者自由泳,剩下的2名运动员四种泳姿都可以承担,则中国队的排兵布阵的方式共有( )
自由泳的接力顺序,每种泳姿100米且由1名运动员完成,且每名运动员都要出场,若中国队确定了备战该项目的4名运动员名单,其中女运动员甲只能承担仰泳或者自由泳,男运动员乙只能承担蝶泳或者自由泳,剩下的2名运动员四种泳姿都可以承担,则中国队的排兵布阵的方式共有( )
A. 144种B. 24种C. 12种D. 6种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆![]() .
.
(1)若椭圆![]() ,判断
,判断![]() 与
与![]() 是否相似?如果相似,求出
是否相似?如果相似,求出![]() 与
与![]() 的相似比;如果不相似,请说明理由;
的相似比;如果不相似,请说明理由;
(2)写出与椭圆![]() 相似且短半轴长为
相似且短半轴长为![]() 的椭圆
的椭圆![]() 的方程;若在椭圆
的方程;若在椭圆![]() 上存在两点
上存在两点![]() 、
、![]() 关于直线
关于直线![]() 对称,求实数
对称,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的参数方程;
的参数方程;
(2)若曲线![]() 与曲线
与曲线![]() ,
,![]() 在第一象限分别交于
在第一象限分别交于![]() 两点,且
两点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com